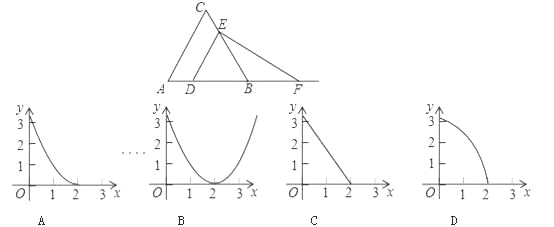
ΧβΡΩΡΎ»ί
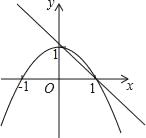
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏy1=©¹x2+1Θ§÷±œΏy2=©¹x+1Θ§Β±x»Έ»Γ“Μ÷Β ±Θ§xΕ‘”ΠΒΡΚ· ΐ÷ΒΖ÷±πΈΣy1Θ§y2Θ°»τy1ΓΌy2Θ§»Γy1Θ§y2÷–ΒΡΫœ–Γ÷ΒΦ«ΈΣMΘΜ»τy1=y2Θ§Φ«M=y1=y2Θ°άΐ»γΘΚΒ±x=2 ±Θ§y1=©¹3Θ§y2=©¹1Θ§y1ΘΦy2Θ§¥Υ ±M=©¹3Θ°œ¬Ν–≈–Εœ÷–ΘΚ
ΔΌΒ±xΘΦ0ΜρxΘΨ1 ±Θ§y1ΘΦy2ΘΜ
ΔΎΒ±xΘΦ0 ±Θ§M=y1ΘΜ
Δέ ΙΒΟM=![]() ΒΡxΒΡ÷Β «©¹
ΒΡxΒΡ÷Β «©¹![]() Μρ
Μρ![]() ΘΜ
ΘΜ
ΔήΕ‘»Έ“βxΒΡ÷ΒΘ§ ΫΉ”![]() =1©¹MΉή≥…ΝΔΘ°
=1©¹MΉή≥…ΝΔΘ°
Τδ÷–’ΐ»ΖΒΡ «_____Θ®Χν…œΥυ”–’ΐ»ΖΒΡΫα¬έΘ©
ΓΨ¥πΑΗΓΩΔΌΔΎΔέΔή
ΓΨΫβΈωΓΩΔΌΙέ≤λΆΦœσΩ…÷ΣΘ§Β±xΘΦ0ΜρxΘΨ1 ±Θ§y1ΘΦy2Θ§Ι ΔΌ’ΐ»ΖΘ§
ΔΎΙέ≤λΆΦœσΩ…÷ΣΘΚΒ±xΘΦ0 ±Θ§M=y1Θ§Ι ΔΎ’ΐ»ΖΘ§
ΔέM=![]() ±Θ§
±Θ§ ![]() =©¹x2+1Θ§ΫβΒΟx=©¹
=©¹x2+1Θ§ΫβΒΟx=©¹![]() Μρ
Μρ![]() Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§
![]() =©¹x+1Θ§ΫβΒΟx=
=©¹x+1Θ§ΫβΒΟx=![]() Θ§
Θ§
ΓύxΒΡ÷Β «©¹![]() Μρ
Μρ![]() Θ§Ι Δέ’ΐ»ΖΘ§
Θ§Ι Δέ’ΐ»ΖΘ§
ΔήΙέ≤λΆΦœσΩ…÷ΣΘΚMΓή1Θ§Ε‘»Έ“βxΒΡ÷ΒΘ§ ΫΉ”![]() =1©¹MΉή≥…ΝΔΘ§Ι Δή’ΐ»ΖΘ§
=1©¹MΉή≥…ΝΔΘ§Ι Δή’ΐ»ΖΘ§
Ι ¥πΑΗΈΣΘΚΔΌΔΎΔέΔήΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 Ά§≤ΫΝΖœΑΚ”Ρœ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
Ά§≤ΫΝΖœΑΚ”Ρœ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ Ά§≤ΫΝΖœΑΈςΡœ ΠΖΕ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
Ά§≤ΫΝΖœΑΈςΡœ ΠΖΕ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ ≤Ι≥δœΑΧβΫ≠Υ’œΒΝ–¥πΑΗ
≤Ι≥δœΑΧβΫ≠Υ’œΒΝ–¥πΑΗ ―ßΝΖΩλ≥ΒΒάΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
―ßΝΖΩλ≥ΒΒάΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ