题目内容
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 在
在![]() 上,点
上,点![]() 在
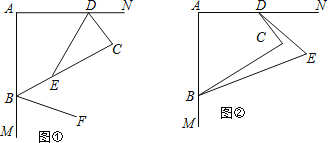
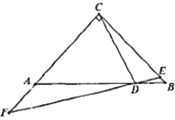
在![]() 的延长线上,连接FD并延长交BC于点E,若∠BED=2∠ADC,AF=2,DF=7,则
的延长线上,连接FD并延长交BC于点E,若∠BED=2∠ADC,AF=2,DF=7,则![]() 的面积为______.
的面积为______.
【答案】![]()
【解析】
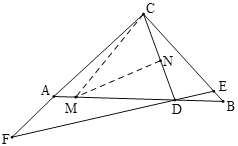
作CD的垂直平分线交AD于M,交CD与N,根据垂直平分线的性质可得MC=MD,进而可得∠MDC=∠MCD,根据已知及外角性质可得∠AMC=∠BED,由等腰直角三角形的性质可得∠B=∠CAB=45°,根据三角形内角和定理可得∠ACM=∠BDE,进而可证明∠ADF=∠ACM,进而即可证明∠FCD=∠FDC,根据等腰三角形的性质可得CF=DF,根据已知可求出AC的长,根据三角形面积公式即可得答案.
作CD的垂直平分线交AD于M,交CD与N,
∵MN是CD的垂直平分线,
∴MC=MD,
∴∠MDC=∠MCD,
∵∠AMC=∠MDC=∠MCD,
∴∠AMC=2∠ADC,
∵∠BED=2∠ADC,
∴∠AMC=∠BED,
∵∠ACB=90°,AC=BC,
∴∠B=∠CAB=45°,
∵∠ACM=180°-∠CAM-∠AMC,∠BDE=180°-∠B-∠BED,
∴∠ACM=∠BDE,
∵∠BDE=∠ADF,
∴∠ADF=∠ACM,
∴∠ADF+∠ADC=∠ACM+∠MCD,即∠FCD=∠FDC,
∴FC=FD,
∵AF=2,FD=7,
∴AC=FC-AF=7-2=5,
∴S△ABC=![]() ×5×5=
×5×5=![]() .
.
故答案为:![]()

练习册系列答案
相关题目