题目内容
【题目】已知二次函数y=4x2﹣4ax+a2﹣2a+2,
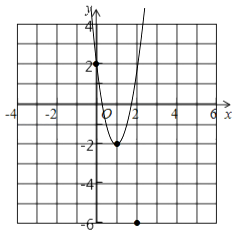
(1)当a=0,2,4时,请在同一直角坐标系中画出对应函数图象的顶点,并画出a=2 时的函数图象;
(2)证明当a取任意实数时,顶点在一条确定的直线上;
(3)求(2)中的直线被抛物线y=4x2﹣4ax+a2﹣2a+2截得的线段长.
【答案】
(1)解:∵二次函数y=4x2﹣4ax+a2﹣2a+2=4(x﹣ ![]() a)2﹣2a+2,
a)2﹣2a+2,
∴抛物线的顶点坐标为( ![]() a,﹣2a+2).
a,﹣2a+2).
当a=0时,抛物线的顶点坐标为(0,2);
当a=2时,抛物线的顶点坐标为(1,﹣2),抛物线的解析式为y=4(x﹣1)2﹣2;
当a=4时,抛物线的顶点坐标为(2,﹣6).
画出函数图象如图所示
(2)证明:∵抛物线的顶点坐标为( ![]() a,﹣2a+2),
a,﹣2a+2),
∴﹣2a+2=﹣4×( ![]() a)+2,
a)+2,
∴y=﹣4x+2,即当a取任意实数时,顶点在一条确定的直线上
(3)解:联立两函数解析式成方程组,
![]() ,解得:
,解得: 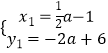 ,
, 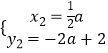 ,
,
∴两函数的交点坐标为( ![]() a﹣1,﹣2a+6),(
a﹣1,﹣2a+6),( ![]() a,﹣2a+2),
a,﹣2a+2),
∴(2)中的直线被抛物线y=4x2﹣4ax+a2﹣2a+2截得的线段长为 ![]() =
= ![]()
【解析】(1) 利用配方法将二次函数解析式由一般式变形为顶点式,由此可得出抛物线的顶点坐标,分别代入a=0、a=2、a=4找出顶点坐标,并画出a=2时,二次函数的图象即可;
(2)由待定系数法,将抛物线的顶点坐标代入直线的解析式,消去a后即可得出y=-4x+2,此题得证;
(3)联立两函数解析式成方程组,通过解方程组求出交点坐标,再根据两点间的距离公式求出线段长度即可.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案