题目内容
【题目】已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= °;
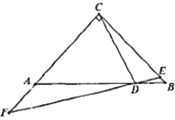
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
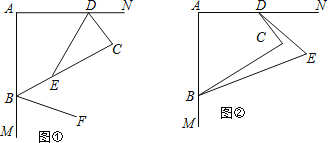
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=![]() ∠CDN,∠CBE=
∠CDN,∠CBE=![]() ∠CBM),试求∠E的度数.
∠CBM),试求∠E的度数.
【答案】(1)180°;(2)DE⊥BF;(3)450
【解析】
(1)根据四边形内角和等于360°列式计算即可得解;
(2)延长DE交BF于G,根据角平分线的定义可得∠CDE=![]() ∠ADC,∠CBF=
∠ADC,∠CBF=![]() ∠CBM,然后求出∠CDE=∠CBF,再利用三角形的内角和定理求出∠BGE=∠C=90°,最后根据垂直的定义证明即可;
∠CBM,然后求出∠CDE=∠CBF,再利用三角形的内角和定理求出∠BGE=∠C=90°,最后根据垂直的定义证明即可;
(3)先求出∠CDE+∠CBE,然后延长DC交BE于H,再根据三角形的一个外角等于与它不相邻的两个内角的和求解即可.
(1)解:∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°-90°×2=180°;
故答案为180°;
(2)解:延长DE交BF于G,
∵DE平分∠ADC,BF平分∠CBM,
∴∠CDE=![]() ∠ADC,∠CBF=
∠ADC,∠CBF=![]() ∠CBM,
∠CBM,
又∵∠CBM=180°-∠ABC=180°-(180°-∠ADC)=∠ADC,
∴∠CDE=∠CBF,
又∵∠BED=∠CDE+∠C=∠CBF+∠BGE,
∴∠BGE=∠C=90°,
∴DG⊥BF,
即DE⊥BF;
(3)解:由(1)得:∠CDN+∠CBM=180°,
∵BE、DE分别四等分∠ABC、∠ADC的外角,
∴∠CDE+∠CBE=![]() ×180°=45°,
×180°=45°,
延长DC交BE于H,
由三角形的外角性质得,∠BHD=∠CDE+∠E,∠BCD=∠BHD+∠CBE,
∴∠BCD=∠CBE+∠CDE+∠E,
∴∠E=90°-45°=45°

练习册系列答案
相关题目