题目内容
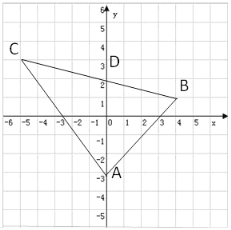
【题目】如图所示的平面直角坐标系中,已知A(0,-3),B(4,1),C(-5,3)
(1) 求三角形ABC的面积;
(2) 点M是平面直角坐标系第一象限内的一动点,点M的纵坐标为3,三角形BCM的面积为6,求点M的坐标;
(3) 记BC与y轴的交点为D,求点D的坐标(写出具体解答过程).
【答案】(1)22;(2)M(1,3);(3) ![]() .
.
【解析】
(1)用矩形的面积减去三个直角三角形的面积即可;
(2)根据三角形BCM的面积为6,求出CM的长,进而可求出点M的坐标;
(3)根据三角形ABC的面积=三角形ABD的面积+三角形ACD的面积,求出AD的长,即可求出点D的坐标.
(1)S△ABC =9×6-![]() = 22;
= 22;
(2)∵![]() ,
,
∴CM=6;
∴点M的横坐标=6-5=1,
∴M(1,3);
(3)∵![]() ,
,
∴AD=![]() ,
,
∴OD= ![]() -3=
-3=![]() ,
,
∴![]() .
.


练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目