题目内容
【题目】如图,AB是⊙O的直径,CO⊥AB于点O,CD是⊙O的切线,切点为D.连接BD,交OC于点E. 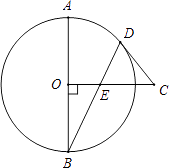
(1)求证:∠CDE=∠CED;
(2)若AB=13,BD=12,求DE的长.
【答案】
(1)证明:连接OD,
∵CD是⊙O的切线,切点为D.
∴∠ODC=90°,
∵OD=OB,∴∠B=∠ODB,
∵OC⊥AB,
∴∠CED=∠OEB=90°﹣∠B,
∵∠CDE=90°﹣∠ODB,
∴∠CDE=∠CED;
(2)连接AD,

∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=13,
∴OB= ![]() ,
,
∵∠ADB=∠BOE,∠B=∠B,
∴△ABD∽△EBO,
∴ ![]() .
.
∴ ![]() ,
,
∴EB= ![]() ,
,
∴DE=BD﹣EB= ![]() .
.
【解析】(1)连接OD,利用切线的性质和圆的半径相等得到的等腰三角形即可证明∠CDE=∠CED;(2)连接AD,利用圆周角定理和已知条件证明△ABD∽△EBO,利用相似三角形的性质即可求出EB的长,进而求出DE的长.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目