题目内容
【题目】如图，在平面直角坐标系xOy中，梯形AOBC的边OB在x轴的正半轴上，AC∥OB，BC⊥OB，过点A的双曲线y= 
的一支在第一象限交梯形对角线OC于点D，交边BC于点E．
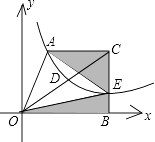
（1）填空：双曲线的另一支在第象限，k的取值范围是；
（2）若点C的坐标为（2，2），当点E在什么位置时，阴影部分的面积S最小？
（3）若 
= 
，S△OAC=2，求双曲线的解析式．
【答案】
（1）三；k＞0
（2）
解：∵梯形AOBC的边OB在x轴的正半轴上，AC∥OB，BC⊥OB，
而点C的坐标为（2，2），
∴A点的纵坐标为2，E点的横坐标为2，B点坐标为（2，0），
把y=2代入y= 
得x= 
；把x=2代入y= 得y= ，
∴A点的坐标为（ ，2），E点的坐标为（2， ），
∴S阴影部分=S△ACE+S△OBE
= 
×（2﹣ ）×（2﹣ ）+ ×2×
= 
k2﹣ k+2
= （k﹣2）2+ 
，
当k﹣2=0，即k=2时，S阴影部分最小，最小值为 ；
∴E点的坐标为（2，1），即E点为BC的中点，
∴当点E在BC的中点时，阴影部分的面积S最小；
（3）
解：设D点坐标为（a， 
），
∵ 
= ，
∴2OD=OC，即D点为OC的中点，
∴C点坐标为（2a， 
），
∴A点的纵坐标为 ，
把y= 代入y= 得x= 
，
∴A点坐标为（ ， ），
∵S△OAC=2，
∴ ×（2a﹣ ）× =2，
∴k= 
，
∴双曲线的解析式为y= 
．
【解析】（1）根据反比例函数图象与性质得到：双曲线y= 的一支在第一象限，则k＞0，得到另一支在第三象限；（2）根据梯形的性质，AC∥x轴，BC⊥x轴，而点C的坐标为（2，2），则A点的纵坐标为2，E点的横坐标为2，B点坐标为（2，0），再分别把y=2或x=2代入y= 可得到A点的坐标为（ ，2），E点的坐标为（2， ），然后计算S阴影部分=S△ACE+S△OBE= ×（2﹣ ）×（2﹣ ）+ ×2× = k2﹣ k+2，配方得 （k﹣2）2+ ，当k=2时，S阴影部分最小值为 ，则E点的坐标为（2，1），即E点为BC的中点；（3）设D点坐标为（a， ），由 = ，则2OD=OC，即D点为OC的中点，于是C点坐标为（2a， ），得到A点的纵坐标为 ，把y= 代入y= 得x= ，确定A点坐标为（ ， ），根据三角形面积公式由S△OAC=2得到 ×（2a﹣ ）× =2，然后解方程即可求出k的值．
