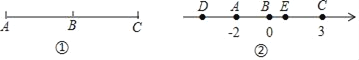��Ŀ����
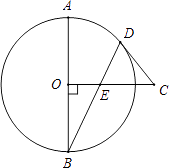
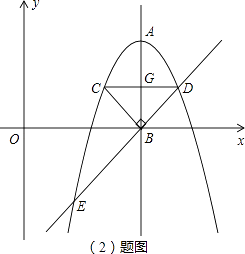
����Ŀ����ͼ��������y=��x2+12x��30�Ķ���ΪA���Գ���AB��x�ύ�ڵ�B����x�Ϸ�������������C��D���㣬���ǹ���AB�Գƣ�����C���ڶԳ������࣬CB��DB��
��1������������ߵĶԳ���Ͷ���A�����ꣻ
��2���������ߵĶԳ������ҳ���Q��ʹ����A��C����ľ�����ȣ��������Q�����ꣻ
��3���ӳ�DB���������ڵ�E�������������Ƿ���ڵ�P��ʹ�á�DEP��������ڡ�DEC������������ڣ�����ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
��ʾ��������y=ax2+bx+c��a��0���ĶԳ���Ϊ ![]() ����������Ϊ
����������Ϊ ![]() ��
��
���𰸡�
��1��
�⣺��y=��x2+12x��30=����x��6��2+6
��������ߵĶԳ���Ϊx=6������A�����꣨6��6����
��2��
�⣺
��C��D����AB�Գƣ�
��BC=BD��CD��x�
�֡�CB��DB��
���BCD�ǵ���ֱ�������Σ�
���DCB=45�㣬����BCGΪ����ֱ�������Σ�CG=BG��
���C�ĺ�����Ϊa����CG=6��a��BG=CG=6��a����C��a��6��a��������y=��x2+12x��30���ã�
6��a=��a2+12a��30����ã�a1=4��a2=9���ᣩ
��C��4��2����
��Q��6��m������AQ=6��m��CQ= ![]()
��AQ=CQ��
��6��m= ![]() ��
��
���m= ![]()
��Q��6�� ![]() ����
����
��3��
�⣺
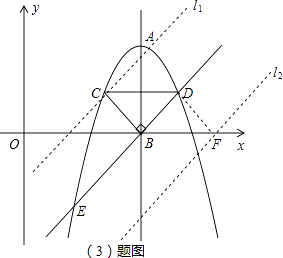
��ֱ��DE�Ľ���ʽ��y=kx+b������D��8��2����B��6��0�����ã�
![]() ��
��
��� ![]()
��ֱ��DE��y=x��6��
����DEP��������ڡ�DEC����������C��P��ֱ��DE�ľ�����ȣ�
�ٹ���C��ֱ��l1��DE�����������ʽΪ��y=x+b1������C��4��2����ã�b1=��2��
����ֱ��l1 y=x��2�����������ߵĽ���ʽ�У�
![]() ��
��
��� ![]() ��
�� ![]()
��P1��7��5����
�ڹ���D��DF��CB����x���ڵ�F�����ı���DCBFΪƽ���ı��Σ����У�DF��DE��BF=CD=4����F��10��0����
����F��ֱ��l2��DE��ͬ�������ֱ��l2��y=x��10�����������ߵĽ���ʽ���У�
![]() ��
��
��� 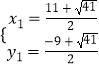 ��
�� 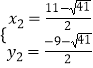
��P2�� ![]() ��
�� ![]() ����P3��
����P3�� ![]() ��
�� ![]() ����
����
���ϣ����������ĵ�P������ΪP1��7��5����P2�� ![]() ��
�� ![]() ����P3��
����P3�� ![]() ��
�� ![]() ����
����
����������1������֪�������߽���ʽ��Ϊ����ʽ�����ɵõ������߶Գ��᷽���Լ���������꣮��2����С������Ҫ�����C�����ꣻ����Rt��CBD��˵��C��D���������߶Գ���Գƣ���CB=BD����ô��CBD�ǵ���ֱ�������Σ����������߶Գ�����CD�Ľ���ΪG����ô��BCGҲ�ǵ���ֱ�������Σ����������C�ĺ����꣬����Rt��BCG��������״��ʾ����C�������꣬���������ߵĽ���ʽ�м��������C�����꣮�����߶Գ�����֪�������Q���������������ϵ�����ľ��빫ʽ��ʾ��CQ��AQ�ij�����CQ=AQ�г����������Q�����꣮��3������DEP����DEC�������ȣ���ô��P���C��ֱ��DE�ľ�����ͬ��
�ٹ���C��ƽ����DE��ֱ�ߣ���ֱ���������ߵĽ���Ϊ���������ĵ�P����ʱ��P��C��ֱ��DE�ľ�����ͬ��
�ڹ���D��DF��BC����x���ڵ�F����ʱ�ı���DCBF��ƽ���ı��Σ���ôDF��DE����DF=BC����ô����F��ֱ��DEƽ�е�ֱ���������ߵĽ���Ҳ�Ƿ��������ĵ�P��

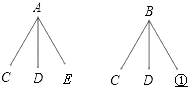
����Ŀ��ij���Ե���A��B�����ͺŵĴ�ӡ����C��D��E����оƬ���ۣ�ÿ���ͺŵĴ�ӡ������Ҫһ��оƬ���ײ��ܴ�ӡ��
��1�������Ǹõ�������ͼ���б���Ƶ����������ٵ�λ��Ӧ��д �� �ڵ�λ��Ӧ ��д
��2��������B�ʹ�ӡ����E��оƬ�����ף������棨1���еķ������׳ɹ�����
оƬ | C | D | E |
A | ��A��C�� | ��A��D�� | �� |
B | ��B��C�� | ��B��D�� | ��B��E�� |