Question

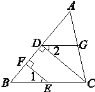
【题目】如图所示，在△ABC中，E，G分别是BC，AC上的点，D，F是AB上的点，已知EF⊥AB，垂足为F，CD⊥AB，垂足为D，∠1＝∠2, 试判断∠AGD和∠ACB是否相等，为什么？

Answer 1

【答案】∠AGD＝∠ACB,理由见解析.

【解析】

根据垂直的定义得到∠BFE=∠BDC=90°，根据平行线的判定方法得到EF∥CD，则∠1=∠ECD，由于∠1=∠2，则∠2=∠ECD，于是可根据平行线的判定方法得到DG∥BC，然后根据平行线的性质即可得到∠AGD=∠ACB．

∠AGD＝∠ACB.

理由如下：

因为EF⊥AB，CD⊥AB(已知)，所以∠EFB＝∠CDB＝90°(垂直的定义)，

所以EF∥CD(同位角相等，两直线平行)，所以∠1＝∠ECD(两直线平行，同位角相等)．又因为∠1＝∠2(已知)，所以∠ECD＝∠2(等量代换)，所以GD∥CB(内错角相等，两直线平行)，所以∠AGD＝∠ACB(两直线平行，同位角相等)．