��Ŀ����
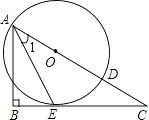
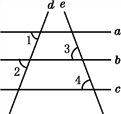
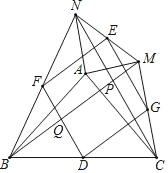
����Ŀ����ͼ������ABC�У�AB=AC����M��N�ֱ���AB��AC�ϵĵ㣬��AM=AN������MN��CM��BN����D��E��F��G�ֱ���BC��MN��BN��CM���е㣬����E��F��D��G��
��l���ж��ı���EFDG����״���� ��������֤������
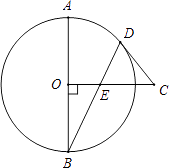
��2���ֽ���AMN�Ƶ�A��תһ���ĽǶȣ������������䣨��ͼ�ڣ����ı���EFDG����״�Ƿ����仯��֤����Ľ��ۣ�
��3����ͼ�ڣ��ڣ�2��������£��뽫��ABC��ԭ�е�����������һ��������ʹ�ı���EFDG�������Σ���д�������ӵ��������������������Ļ�����֤���ı���EFDG�������Σ�

���𰸡���1�����Σ���2�����䣬֤������������3��������������BAC=90�㣬֤��������.
��������
(1) �ı���EFDG��ƽ���ı���, ����Ϊ: ��ͼ1,����AM,��E��F,G��H�ֱ�Ϊ�е�,����������λ�߶����õ�����Ա����, ���ɵ�֤;
(2) ��ͼ��, ����ת�á�BAM=��CAN, ��BAM�ա�CAN��SAS��, BM=CN����E��F�ֱ���MN��BN���е�,�ɵ�EF��DG��EF=DG���ɵ��ı���EFDG��ƽ���ı��Σ��ɵ�FD=![]() BM=EF�������ı���EFDG������;
BM=EF�������ı���EFDG������;
(3) ��BM��CN���ڵ�P��DF��BM���ڵ�Q���ɡ�ABM=��CAN����ABC+��ACB=90��ɵá�BPC=90�㣬��BQD=90�㣬��FDG=90�㣬��������EFDG��������.
�⣺��1���ı���EFDG�����Σ�
�ߵ�D��E��F��G�ֱ���BC��MN��BN��CM���е㣬
��EF�ǡ�NBM����λ�ߣ�DG�ǡ�CBM����λ�ߣ�EG�ǡ�CMN����λ�ߣ�DF�ǡ�BCN����λ�ߣ�
��EF=DG=![]() BM��EG=DF=
BM��EG=DF=![]() CN��
CN��
��AB=AC��AM=AN��
��BM=CN��
��EF=DF=EG=DG��
���ı���EFDG�����Σ�
�ʴ�Ϊ�����Σ�
��2�����䣬
֤��������ת�á�BAM=��CAN��
�ڡ�BAM�͡�CAN�У�
��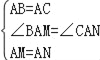 ��
��
���BAM�ա�CAN��SAS����
��BM=CN��
�ߵ�E��F�ֱ���MN��BN���е㣬
��EF��BM��EF=![]() BM��
BM��
ͬ����DG��BM��DG=![]() BM��FD=
BM��FD=![]() CN��
CN��
��EF��DG��EF=DG��
���ı���EFDG��ƽ���ı��Σ�
��EF��CN��BM=CN��
��FD=![]() BM=EF��
BM=EF��
���ı���EFDG�����Σ�
��3��������������BAC=90�㣬
֤������ͼ����BM��CN���ڵ�P��DF��BM���ڵ�Q��
�ɣ�2���á�ABM=��ACN��
�ߡ�BAC=90�㣬
���ABC+��ACB=90�㣬
�ࣨ��ABC����ABM��+����ACB+��ACN��=90�㣬����PBC+��PCB=90�㣬
���BPC=90�㣬
��DF��CN��
���BQD=90�㣬
��DG��BM��
���FDG=90�㣬
������EFDG��������