题目内容
【题目】![]() 问题发现
问题发现
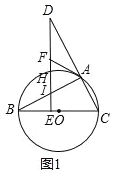
在等腰三角形ABC中,![]() ,分别以AB和AC为斜边,向
,分别以AB和AC为斜边,向![]() 的外侧作等腰直角三角形,如图1所示,其中
的外侧作等腰直角三角形,如图1所示,其中![]() 于点F,
于点F,![]() 于点G,M是BC的中点,连接MD和ME.
于点G,M是BC的中点,连接MD和ME.
填空:线段AF,AG,AB之间的数量关系是______;
线段MD,ME之间的数量关系是______.
![]() 拓展探究
拓展探究
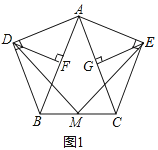
在任意三角形ABC中,分别以AB和AC为斜边向![]() 的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?并说明理由;
的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?并说明理由;
![]() 解决问题
解决问题
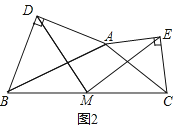
在任意三角形ABC中,分别以AB和AC为斜边,向![]() 的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,若
的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,若![]() ,请直接写出线段DE的长.
,请直接写出线段DE的长.
【答案】![]()
![]()
【解析】
(1)由条件可以通过三角形全等和轴对称的性质,直角三角形的性质得出结论;
(2)取AB、AC的中点F、G,连接DF,MF,EG,MG,根据三角形的中位线的性质和等腰直角三角形的性质就可以得出四边形AFMG是平行四边形,从而得出△DFM≌△MGE,根据其性质就可以得出结论;
(3)取AB、AC的中点F、G,连接DF,MF,EG,MG,DF和MG相交于H,根据三角形的中位线的性质K可以得出△DFM≌△MGE,由全等三角形的性质和勾股定理就可以得出答案.
![]() ,理由如下:
,理由如下:
![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,![]()
![]() 在
在![]() 和
和![]() 中,
中,
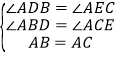 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() 于点F,
于点F,![]() 于点G,
于点G,
![]() ,
,![]() .
.
![]() ,
,
![]() ;
;
![]() ,理由如下:
,理由如下:
![]() 是BC的中点,
是BC的中点,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
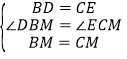 ,
,
![]() ≌
≌![]() ,
,
![]() ;
;
故答案为:![]() ;
;![]() ;
;
![]() ,
,![]() .
.
理由如下:
取AB,AC的中点F,G,连接DF,FM,MG,EG,设AB与DM交于点H,如图2,

![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,![]() ,
,![]() .
.
![]() 点M是BC的中点,
点M是BC的中点,
![]() 和MG都是
和MG都是![]() 的中位线,
的中位线,
![]() ,
,![]() ,
,
![]() 四边形AFMG是平行四边形,
四边形AFMG是平行四边形,
![]() ,
,![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,即
,即![]() ;
;
![]() 线段DE的长为
线段DE的长为![]() ,理由如下:
,理由如下:
分别取AB,AC的中点F,G,连接MF,DF,MG,EG,设DF和MG交于点H,如图3,
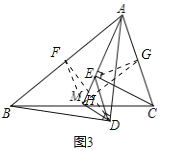
![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,![]() ,
,![]() .
.
![]() 点M是BC的中点,
点M是BC的中点,
![]() 和MG都是
和MG都是![]() 的中位线,
的中位线,
![]() ,
,![]() ,
,
![]() 四边形AFMG是平行四边形,
四边形AFMG是平行四边形,
![]() ,
,![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
![]() ≌
≌![]() .
.
![]() ,
,![]() .
.
![]() 即
即![]() .
.
又![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
在![]() 中,
中,![]() ,由勾股定理,得
,由勾股定理,得![]() .
.

【题目】为保护和改善环境,发展新经济,国家出台了不限行、不限购等诸多新能源汽车优惠政策鼓励新能源汽车的发展,为响应号召,某市某汽车专卖店销售A,B两种型号的新能源汽车共25辆,这两种型号的新能源汽车的进价、售价如下表:
进价 | 售价 | |
A型 | 10 |
|
B型 | 15 |
|
![]() 如何进货,进货款恰好为325万元?
如何进货,进货款恰好为325万元?
![]() 如何进货,该专卖店售完A,B两种型号的新能源汽车后获利最多且不超过进货价的
如何进货,该专卖店售完A,B两种型号的新能源汽车后获利最多且不超过进货价的![]() ,此时利润为多少元?
,此时利润为多少元?