题目内容
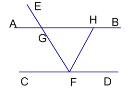
【题目】如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数. 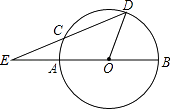
【答案】解:连结OC,如图,
∵CE=AO,
而OA=OC,
∴OC=EC,
∴∠E=∠1,
∴∠2=∠E+∠1=2∠E,
∵OC=OD,
∴∠D=∠2=2∠E,
∵∠BOD=∠E+∠D,
∴∠E+2∠E=75°,
∴∠E=25°.
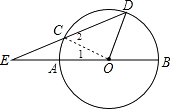
【解析】连结OC,如图,由CE=AO,OA=OC得到OC=EC,则根据等腰三角形的性质得∠E=∠1,再利用三角形外角性质得∠2=∠E+∠1=2∠E,加上∠D=∠2=2∠E,
所以∠BOD=∠E+∠D,即∠E+2∠E=75°,然后解方程即可.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对圆的定义的理解,了解平面上到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心,定长称为半径.

练习册系列答案
相关题目