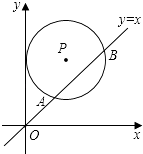题目内容
【题目】如图,直线y= ![]() +3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为cm2 .
+3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为cm2 . 
【答案】11
【解析】解:如图,
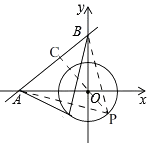
∵直线y= ![]() +3与坐标轴交于A、B两点,
+3与坐标轴交于A、B两点,
∴A(﹣4,0),B(0,3),
∴OA=4,OB=3,
在Rt△AOB中,根据勾股定理得,AB=5,
∵△PAB中,AB=5是定值,
∴要使△PAB的面积最大,即⊙O上的点到AB的距离最大,
∴过点O作OC⊥AB于C,CO的延长线交⊙O于P,此时S△PAB的面积最大,
∴S△AOB= ![]() OAOB=
OAOB= ![]() ABOC,
ABOC,
∴OC= ![]() ,
,
∵⊙O的半径为2,
∴CP=OC+OP= ![]() ,
,
∴S△PAB= ![]() ABCP=
ABCP= ![]() ×5×
×5× ![]() =11.
=11.
所以答案是11.
【考点精析】通过灵活运用圆的定义和切线的性质定理,掌握平面上到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心,定长称为半径;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
【题目】某汽车行驶时油箱中余油量Q(升)与行驶时间t(小时)的关系如下表:
行驶时间t | 1 | 2 | 3 | 4 | … |
余油量Q | 40﹣6 | 40﹣12 | 40﹣18 | 40﹣24 | … |
(1)写出用行驶时间t表示余油量Q的代数式 ;
(2)当t=![]() 时,余油量Q的值为 升;
时,余油量Q的值为 升;
(3)汽车每小时行驶60公里,问油箱中原有汽油可供汽车行驶多少公里?