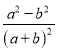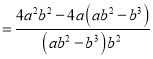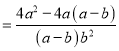题目内容
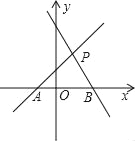
【题目】如图，直线PA是一次函数y＝x+1的图象，直线PB是一次函数y＝﹣2x+2的图象．
（1）求A、B、P三点坐标．
（2）求△PAB的面积．
【答案】（1）A点坐标为（﹣1，0）；B点坐标为（1，0）；P点坐标为（
，
）；（2）．
【解析】
试题（1）根据x轴上点的坐标特征把y=0分别代入y=x+1和y=﹣2x+2，求出对应的自变量的值即可得到A和B点坐标；通过解方程组
可确定P点坐标；
（2）利用三角形面积公式计算．
解：（1）把y=0代入y=x+1得x+1=0，解得x=﹣1，则A点坐标为（﹣1，0）；
把y=0代入y=﹣2x+2得﹣2x+2=0，解得x=1，则B点坐标为（1，0）；
解方程组得
，
所以P点坐标为（，）；
（2）S△PAB=
×（1+1）×=．
练习册系列答案
相关题目
