题目内容
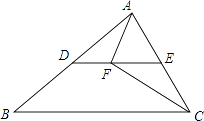
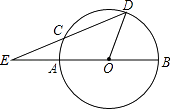
【题目】如图所示,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,EF⊥AB,垂足为F,且AB=DE.

(1)求证:△BCD是等腰直角三角形;
(2)若BD=8厘米,求AC的长.
【答案】(1)略 (2)4cm
【解析】
(1)要证△BCD是等腰直角三角形,只需证BC=DB,由已知BD⊥BC,EF⊥AB,可证∠2=∠3,由已知AC⊥BC,DB⊥BC,可证AC∥BD,得∠A=∠2,即可证得∠A=∠3,又已知∠ACB=∠EBD=90°,AB=DE,符合三角形全等的判定定理AAS,即可证得△ACB≌△EBD,所以BC=DB,即证△BCD是等腰直角三角形;
(2)由(1)知△ACB≌△EBD,得到AC=EB,又因为BD=8cm,即BC=8cm.又因为E是BC中点,故BE=4,即可求AC=4cm.
(1)如图所示,
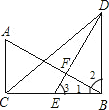
∵BD⊥BC,EF⊥AB,
∴∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
∵AC⊥BC,DB⊥BC,
∴AC∥BD,
∴∠A=∠2,
∴∠A=∠3,
∴又∠ACB=∠EBD=90°,AB=DE,
∴△ACB≌△EBD,
∴BC=DB,
∴△BCD是等腰直角三角形;
(2)由△ACB≌△EBD,
∴AC=EB,
∵BD=8cm,
∴BC=8cm.
∵E是BC中点,
∴BE=4cm,
∴AC=4(cm).

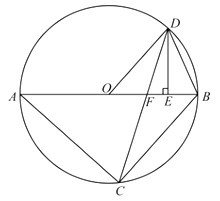
【题目】如图,已知 ![]() 内接于
内接于 ![]() ,
, ![]() 是直径,点
是直径,点 ![]() 在
在 ![]() 上,
上, ![]() ,过点
,过点 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,连接
,连接 ![]() 交
交 ![]() 边于点
边于点 ![]() .
.
(1)求证: ![]() ∽
∽ ![]() ;
;
(2)求证: ![]() ;
;
(3)连接 ![]() ,设
,设 ![]() 的面积为
的面积为 ![]() ,四边形
,四边形 ![]() 的面积为
的面积为 ![]() ,若
,若 ![]() ,求
,求 ![]() 的值.
的值.
【题目】某汽车行驶时油箱中余油量Q(升)与行驶时间t(小时)的关系如下表:
行驶时间t | 1 | 2 | 3 | 4 | … |
余油量Q | 40﹣6 | 40﹣12 | 40﹣18 | 40﹣24 | … |
(1)写出用行驶时间t表示余油量Q的代数式 ;
(2)当t=![]() 时,余油量Q的值为 升;
时,余油量Q的值为 升;
(3)汽车每小时行驶60公里,问油箱中原有汽油可供汽车行驶多少公里?