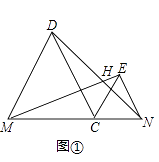
题目内容
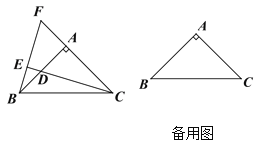
【题目】如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
【答案】(1)证明:在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,
∴△ACD≌△ABE,
∴AD=AE.
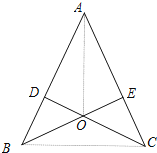 (2)互相垂直,
(2)互相垂直,
在Rt△ADO与△AEO中,
∵OA=OA,AD=AE,
∴△ADO≌△AEO,
∴∠DAO=∠EAO,
即OA是∠BAC的平分线,
又∵AB=AC,
∴OA⊥BC.
【解析】
试题(1)根据AAS推出△ACD≌△ABE,根据全等三角形的性质得出即可;
(2)证Rt△ADO≌Rt△AEO,推出∠DAO=∠EAO,根据等腰三角形的性质推出即可.
试题解析:(1)证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
△ACD和△ABE中,
∵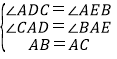
∴△ACD≌△ABE(AAS),
∴AD=AE.
(2)猜想:OA⊥BC.
证明:连接OA、BC,
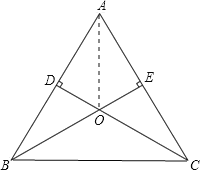
∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°.
在Rt△ADO和Rt△AEO中,
∵![]()
∴Rt△ADO≌Rt△AEO(HL).
∴∠DAO=∠EAO,
又∵AB=AC,
∴OA⊥BC.

练习册系列答案
相关题目