题目内容
【题目】阅读理解填空，并在括号内填注理由．
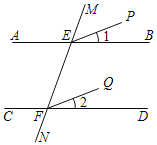
如图，已知AB∥CD，M，N分别交AB，CD于点E，F，∠1＝∠2，求证：EP∥FQ．
证明：∵AB∥CD（ ）
∴∠MEB＝∠MFD（ ）．
又∵∠1＝∠2（ ）
∠MEB﹣∠1＝∠MFD﹣∠2（ ）
即：∠MEP＝∠
EP∥ ．（ ）
【答案】已知，两直线平行同位角相等，已知，角的和差定义，MFQ，FQ，同位角相等两直线平行．
【解析】
根据平行线的判定和性质进行证明即可．
解：∵AB∥CD（已知）
∴∠MEB＝∠MFD（两直线平行同位角相等）．
又∵∠1＝∠2（已知）
∠MEB﹣∠1＝∠MFD﹣∠2（角的和差定义）
即：∠MEP＝∠MFQ
EP∥FQ．（同位角相等两直线平行）
故答案为：已知，两直线平行同位角相等，已知，角的和差定义，MFQ，FQ，同位角相等两直线平行．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某汽车行驶时油箱中余油量Q（升）与行驶时间t（小时）的关系如下表：
行驶时间t | 1 | 2 | 3 | 4 | … |
余油量Q | 40﹣6 | 40﹣12 | 40﹣18 | 40﹣24 | … |
（1）写出用行驶时间t表示余油量Q的代数式 ；
（2）当t=
时，余油量Q的值为 升；
（3）汽车每小时行驶60公里，问油箱中原有汽油可供汽车行驶多少公里？
