题目内容
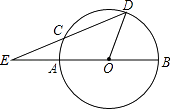
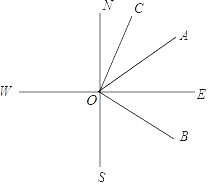
【题目】如图,直线SN⊥直线WE,垂足是点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
(1)写出图中与∠BOE互余的角: .
(2)若射线OA是∠BON的角平分线,探索∠BOS与∠AOC的数量关系.
【答案】(1)∠BOS,∠COE;(2)∠AOC=![]() ∠BOS.
∠BOS.
【解析】
(1)由图直接可知与∠BOE互余的角为∠BOS,∠BOS+∠CON+∠BOE+COE=180°,再由m°的角与n°的角互余可得∠BOE+∠COE=90°,据此可进行解答;
(2)由射线OA是∠BON的角平分线可得∠NOA=![]() ∠NOB,再由∠BOS与∠BON互补可求得∠NOA=
∠NOB,再由∠BOS与∠BON互补可求得∠NOA=![]() ∠BON=
∠BON=![]() (180°﹣∠BOS)=90°﹣
(180°﹣∠BOS)=90°﹣![]() ∠BOS;由∠NOC与∠BOS互余可得∠AOC=∠NOA﹣∠NOC=90°﹣
∠BOS;由∠NOC与∠BOS互余可得∠AOC=∠NOA﹣∠NOC=90°﹣![]() ∠BOS﹣(90°﹣∠BOS)=
∠BOS﹣(90°﹣∠BOS)=![]() ∠BOS.
∠BOS.
解:(1)首先与∠BOE互余的角有∠BOS,
由m°的角与n°的角互余知∠BOS+∠CON=90°,
∵∠BOS+∠CON+∠BOE+COE=180°,
∴∠BOE+∠COE=90°,
与∠BOE互余的角有∠BOS,∠COE,
故答案为:∠BOS,∠COE;
(2)∠AOC=![]() ∠BOS.
∠BOS.
∵射线OA是∠BON的角平分线,
∴∠NOA=![]() ∠NOB,
∠NOB,
∵∠BOS+∠BON=180°,
∴∠BON=180°﹣∠BOS,
∠NOA=![]() ∠BON=90°﹣
∠BON=90°﹣![]() ∠BOS,
∠BOS,
∵∠NOC+∠BOS=90°,∠NOC=90°﹣∠BOS,
∴∠AOC=∠NOA﹣∠NOC=90°﹣![]() ∠BOS﹣(90°﹣∠BOS)=
∠BOS﹣(90°﹣∠BOS)=![]() ∠BOS
∠BOS
∴∠AOC=![]() ∠BOS.
∠BOS.

练习册系列答案
相关题目