题目内容
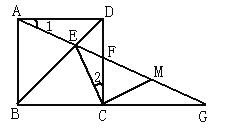
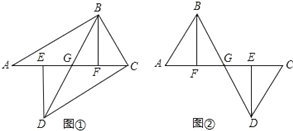
【题目】如图①,A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD.
(1)图①中有 对全等三角形,并把它们写出来 ;
(2)求证:BG=DG,AG=CG;
(3)若将△ABF的边AF沿GA方向移动变为图②时,其余条件不变,第(2)题中的结论是否成立,如果成立,请予证明.
【答案】(1)3对,△AFB≌△DEC,△DEG≌△BFG,△AGB≌△CGD;(2)证明见解析;(3)成立,证明见解析.
【解析】
试题(1)利用A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD可判断全等三角形的个数.
(2)先根据DE⊥AC,BF⊥AC,AE=CF,求证△ABF≌△CDE,再求证△DEG≌△BFG,即可.
(3)先根据DE⊥AC,BF⊥AC,AE=CF,求证△ABF≌△CED,再求证△BFG≌△DEG,即可得出结论.
试题解析:(1)图①中有3对全等三角形,它们是△AFB≌△DEC,△DEG≌△BFG,△AGB≌△CGD.
理由:∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在Rt△ABF和Rt△CDE中,
![]()
∴Rt△ABF≌Rt△CED(HL),
∴ED=BF.
由∠AFB=∠CED=90°得DE∥BF,
∴∠EDG=∠GBF,
∵∠EGD和∠FGB是对顶角,ED=BF,
∴△DEG≌△BFG,
∴EG=FG,DG=BG,
∵∠AGB=∠CGD,
∴△AGB≌△CGD;
(2)∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在Rt△ABF和Rt△CDE中,
![]()
∴Rt△ABF≌Rt△CED(HL),
∴ED=BF.
由∠AFB=∠CED=90°得DE∥BF,
∴∠EDG=∠GBF,
∵∠EGD和∠FGB是对顶角,ED=BF,
∴△DEG≌△BFG,
∴EG=FG,DG=BG,
(3)第(2)题中的结论成立,
理由:∵AE=CF,
∴AE-EF=CF-EF,即AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
在Rt△ABF和Rt△CDE中,
![]()
∴Rt△ABF≌Rt△CED(HL),
∴BF=ED.
∵∠BFG=∠DEG=90°,
∴BF∥ED,
∴∠FBG=∠EDG,
∴△BFG≌△DEG,
∴FG=GE,BG=GD,
即第(2)题中的结论仍然成立.