��Ŀ����
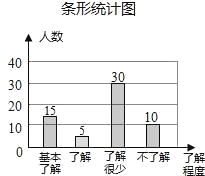
����Ŀ��������9�֣��ݱ����������ʼ���ʯͷ��Э�������齫������ʯͷ������Ϊ���˻������Ŀ��ijУѧ������֪��ѧ�������������˽�̶ȣ������ȡ����ѧ��������һ���ʾ����飬�������ռ�������Ϣ������ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺
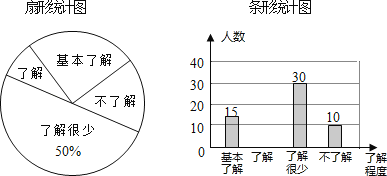
��1�������ʾ������ѧ������___��������ͳ��ͼ���������˽�����������Ӧ���ε�Բ�Ľ�Ϊ___���벹ȫ����ͳ��ͼ��
��2������У����ѧ��900�ˣ���������������������Ƹ�Уѧ���жԽ�������ʯͷ������Ϊ���˻������Ŀ������ﵽ���˽������������˽����̶ȵ���������
��3��������ʯͷ��������ʱ˫��ÿ�������������������ʯͷ���������������������е�һ�֣�����Ϊ������ʤ������ʤʯͷ��ʯͷʤ��������˫��������ͬ���ƣ������ƽ����С�պ�С������ֻ����һ�֣�������״ͼ���б��������˴�ƽ�ĸ��ʣ�
���𰸡���1��60��90����ͳ��ͼ�����������2��300����3��![]() ��
��
�������������������1�������˽����������������ռ�İٷֱȵó�ѧ������������������˽�����ѧ��ռ�İٷֱȣ�����360�õ��������ȫ����ͳ��ͼ���ɣ�
��2��������˽������������˽����̶ȵİٷֱ�֮�ͣ�����900���ɵõ������
��3���б��ó����еȿ��ܵ���������ҳ����˴�ƽ��������������������ĸ��ʣ�
�����������1����������ã�30��50%=60�����������˽�������Ϊ60����15+30+10��=5��������
�������˽���ռ�İٷֱ�Ϊ![]() ��100%=25%��ռ�ĽǶ�Ϊ25%��360��=90����
��100%=25%��ռ�ĽǶ�Ϊ25%��360��=90����
��ȫ����ͳ��ͼ��ͼ��ʾ��
��2����������ã�900��![]() =300���ˣ���
=300���ˣ���
����Ƹ�Уѧ���жԽ�������ʯͷ������Ϊ���˻������Ŀ������ﵽ���˽������������˽����̶ȵ�������Ϊ300�ˣ�
��3���б����£�
�� ʯ ��
�� ���������� ��ʯ������ ����������
ʯ ������ʯ�� ��ʯ��ʯ�� ������ʯ��
�� ���������� ��ʯ������ ����������
���еȿ��ܵ������9�֣��������˴�ƽ�������3�֣�
��P=![]() =
=![]() ��
��

 ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д�