题目内容
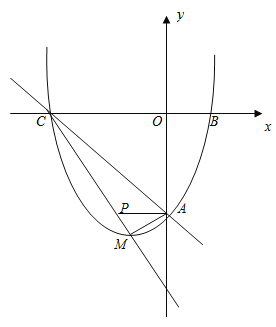
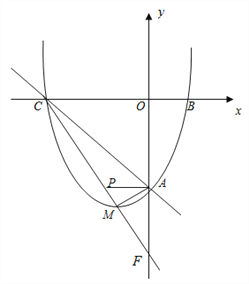
【题目】如图，已知抛物线y=ax2+bx+c与x轴交于点B，C，与直线AC:y=－x－6交y轴于点A，点M是抛物线的顶点，且横坐标为－2.
（1）求出抛物线的表达式.
（2）判断△ACM的形状并说明理由.
（3）直线CM交y轴于点F，在直线CM上是否存在一点P，使∠CMA=∠PAF，若存在，求出P的坐标，若不存在，说明理由.
【答案】（1）
；（2）△ACM为直角三角形，理由见解析；（3）存在， 
， 
【解析】解：（1） A（0，－6） C（－6，0）
∴
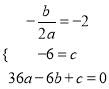
解得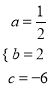
∴此抛物线的表达式为
.
（2）△ACM为直角三角形，理由如下：
M（－2，－8）
∴AC2+AM2=72+22+（8－6）2=80
MC2=42+82=80
∴AC2+AM2=MC2
∴△ACM为直角三角形
（3）假设存在
设直线CM的解析式为y=kx+b过C（－6，0）、M（－2，－8）则
解得
∴y=－2x－12
设P(n,－2n－12)
∴∠CMA=∠MAF+∠AFM ∠PAF=∠MAF+∠PAM
又 ∠APF=∠MPA ∴ △APF～△MPA
∴
即
∴
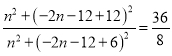
∴ 35n2+216n+324=0
∴
， 
∴ 符合条件的P点有两个,其坐标分别为 ：
， 
练习册系列答案
相关题目
