Question

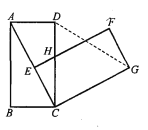
【题目】如图，在矩形ABCD中，AB＝4，BC＝3，将矩形绕点C按顺时针方向旋转，使点B落在线段AC上，得矩形CEFG，边CD与EF交于点H，连接DG．

(1)CH＝ ．

(2)求DG的长．

Answer 1

【答案】(1) ；(2)；

【解析】

试题分析：（1）利用勾股定理列式求出AC，根据旋转的性质可得CE=BC，然后根据△ABC和△CEH相似，利用相似三角形对应边成比例列式求解即可；

（2）过点G作GM⊥CD于M，然后求出△ABC和△GMC相似，根据相似三角形对应边成比例求出CM、MG，再求出DM，然后利用勾股定理列式计算即可得到DG．

试题解析：（1）在矩形ABCD中，∵AB=4，BC=3，

∴AC=，

∵矩形ABCD绕点C按顺时针方向旋转得矩形CEFG，

∴CE=BC=3，

∵∠BAC+∠ACB=90°，∠ECH+∠ACB=90°，

∴∠BAC=∠ECH，

又∵∠B=∠CEH=90°，

∴△ABC∽△CEH，

∴，

即

解得；

（2）如图，过点G作GM⊥CD于M，

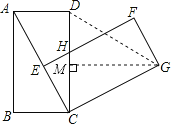
∵∠ACB+∠ACD=∠GCM+∠ACD=90°，

∴∠ACB=∠GCM，

又∵∠B=∠GMC=90°，

∴△ABC∽△GMC，

∴，

即，

解得CM=，MG=，

∴DM=CD-CM=4-=，

在Rt△DMG中，DG=．