Question

【题目】已知：如图，∠ABC和∠ACB的平分线交于点O，EF经过点O且平行于BC，分别与AB，AC交于点E，F．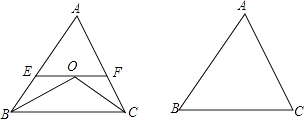

（1）若∠ABC=50°，∠ACB=60°，求∠BOC的度数；
（2）若∠ABC=α，∠ACB=β，用α，β的代数式表示∠BOC的度数．
（3）在第（2）问的条件下，若∠ABC和∠ACB邻补角的平分线交于点O，其他条件不变，请画出相应图形，并用α，β的代数式表示∠BOC的度数．

Answer 1

【答案】
（1）

解：∵∠ABC和∠ACB的平分线交于点O，∠ABC=50°，∠ACB=60°，

∴∠OBC+∠OCB= （∠ABC+∠ACB）= ×（50°+60°）=55°，

∴∠BOC=180°﹣（∠OBC+∠OCB）=180°﹣55°=125°

（2）

解：∵∠ABC和∠ACB的平分线交于点O，∠ABC=α，∠ACB=β，

∴∠OBC+∠OCB= （∠ABC+∠ACB）= （α+β），

∴∠BOC=180°﹣（∠OBC+∠OCB）=180°﹣ （α+β）

（3）

解：如图所示：

∵∠ABC和∠ACB邻补角的平分线交于点O，

∴∠CBO+∠BCO= + =180°﹣ ，

∴∠BOC=180°﹣（180°﹣ ）= α+ β．

【解析】（1）先根据角平分线的定义求出∠OBC+∠OCB的度数，再根据三角形内角和定理求出∠BOC的度数即可；（2）先用α、β表示出∠OBC+∠OCB的度数，再根据三角形内角和定理求出∠BOC的度数即可；（3）根据题意画出图形，再根据三角平分线的定义求出∠CBO+∠ACO的度数，进而可得出结论．
【考点精析】利用平行线的性质和三角形的内角和外角对题目进行判断即可得到答案，需要熟知两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．