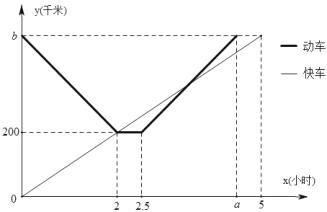
题目内容
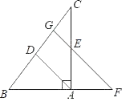
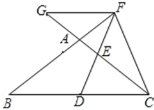
【题目】如图,在△ABC 中,AB =AC,点D在BC上,点F在BA的延长线上,FD =FC,点E是AC与DF的交点,且ED =EF,FG∥BC交CA的延长线于点G.
(1)∠BFD =∠GCF 吗?说明理由;
(2)求证:△GEF ≌△CED;
(3)求证:BD =DC.
【答案】(1)∠BFD=∠GCF,理由见解析;(2)证明见解析;(3)证明见解析
【解析】
(1)根据AB=AC得出∠B=∠BCA,再利用FD=FC得出∠FDC=∠DCF,最后结合三角形外角性质进一步证明即可;
(2)利用平行线性质得出∠GFE=∠CDE,然后结合题意根据“ASA”进一步证明结论即可;
(3)首先根据题意得出∠B=∠G,然后进一步证明△GFC△BDF,由此得出GF=BD,再根据△GEF△CED得出GF=CD,据此进一步证明结论即可.
(1)∠BFD=∠GCF,理由如下:
∵AB=AC,
∴∠B=∠BCA,
∵FD=FC,
∴∠FDC=∠DCF,
∵∠BFD=∠FDC∠B,∠GCF=∠DCF∠BCA,
∴∠BFD=∠GCF;
(2)∵FG∥BC,
∴∠GFE=∠CDE,
在△GEF和△CED中,
∵∠GFE=∠CDE,ED=EF,∠FEG=∠DEC,
∴△GEF△CED(ASA);
(3)∵FG∥BC,
∴∠G=∠BCA,
∵∠B=BCA,
∴∠B=∠G,
在△GFC和△BDF中,
∵∠B=∠G,∠BFD=∠GCF,FD=FC,
∴△GFC△BDF(AAS),
∴GF=BD,
∵△GEF△CED,
∴GF=CD,
∴BD=DC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目