题目内容
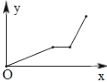
【题目】某地区在同一直线上依次有甲、乙、丙三座城市一列快车从甲市出发匀速行驶开往丙市,一列动车从丙市出发匀速行驶往返于乙、丙两座城市,两列火车同时出发.如图是两列火车距甲市的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数图象,请你结合图像信息解决下列问题:
(小时)之间的函数图象,请你结合图像信息解决下列问题:
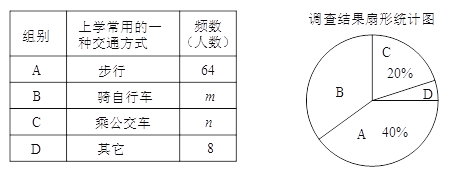
(1)直接写出:甲、乙两市相距 千米,图像中![]() 的值为 ,
的值为 ,![]() 的值 ;
的值 ;
(2)求动车从乙地返回多长时间时与快车相遇?
(3)请直接写出快车出发多长时间两列火车(都在行驶时)相距30千米?
【答案】(1)200,4.5,500;(2)1小时;(3)快车出发1.88小时或2.9小时或4.1小时两列火车(都在行驶时)相距30千米
【解析】
(1)由图可知:当x=2时,y=200,此时动车停在乙市,所以甲、乙两市相距200千米,动车从丙市出发匀速行驶往返于乙、丙两座城市,动车从丙市出发匀速行驶到乙市所用的时间与动车从乙市出发匀速行驶到丙市所用的时间相同,都为2小时,可得a=2.5+2=4.5,快车2小时行驶了200千米,可求得快车速度,
b=100×5=500
(2)设快车距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=kx,
把点(2,200)的坐标代入到y=kx中,求得函数解析式y=100x.
设动车从乙地返回时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=k1x+b1,把点(2.5,200)、(4.5,500)的坐标分别代入到y=k1x+b1中,求得函数解析式y=150x-175,求出方程组![]() 的解为
的解为![]() ,因为3.5-2.5=1(小时),可得动车从乙地返回1小时时与快车相遇.
,因为3.5-2.5=1(小时),可得动车从乙地返回1小时时与快车相遇.
(3)设动车丙市出发时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=k2x+b2,把点(2,200)、(0,500)的坐标分别代入到y=k2x+b2中,解得y=-150x+500,由(2)可知:快车距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=100x(0≤x≤5),动车从乙地返回时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=150x-175(2.5≤x≤4.5),
当0≤x≤2时,-150x+500-100x=30,解得x=![]() =1.88;
=1.88;
当2.5≤x≤3.5时,100x-(150x-175)=30,解得x=![]() =2.9;
=2.9;
当3.5≤x≤4.5时,150x-175-100x=30,解得x=![]() =4.1
=4.1
综上所述,快车出发1.88小时或2.9小时或4.1小时两列火车(都在行驶时)相距30千米.
(1)由图可知:当x=2时,y=200,此时动车停在乙市
∴甲、乙两市相距200千米,
∵动车从丙市出发匀速行驶往返于乙、丙两座城市,
∴动车从丙市出发匀速行驶到乙市所用的时间与动车从乙市出发匀速行驶到丙市所用的时间相同,都为2小时,
∴a=2.5+2=4.5
由图可知:快车2小时行驶了200千米
∴快车的速度为:200÷2=100(千米/时)
∴100×5=500(千米)
∴b=500
故答案为:200,4.5,500
(2)设快车距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=kx,
把点(2,200)的坐标代入到y=kx中,
得:200=2k,
解得k=100,
∴快车距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=100x(0≤x≤5),
设动车从乙地返回时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=k1x+b1,把点(2.5,200)、(4.5,500)的坐标分别代入到y=k1x+b1中,得: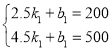 ,
,
解得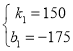 ,
,
∴动车从乙地返回时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=150x-175(2.5≤x≤4.5),
∵方程组![]() 的解为
的解为![]()
∴3.5-2.5=1(小时)
∴动车从乙地返回1小时时与快车相遇;
(3)设动车丙市出发时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=k2x+b2,把点(2,200)、(0,500)的坐标分别代入到y=k2x+b2中,得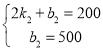 ,
,
解得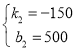 ,
,
∴动车丙市出发时,距甲市的路程(千米)与行驶时间(小时)之间的函数关系式为y=-150x+500,
由(2)可知:快车距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=100x(0≤x≤5)
动车从乙地返回时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=150x-175(2.5≤x≤4.5),
当0≤x≤2时,-150x+500-100x=30,解得x=![]() =1.88;
=1.88;
当2.5≤x≤3.5时,100x-(150x-175)=30,解得x=![]() =2.9;
=2.9;
当3.5≤x≤4.5时,150x-175-100x=30,解得x=![]() =4.1
=4.1
综上所述,快车出发1.88小时或2.9小时或4.1小时两列火车(都在行驶时)相距30千米.

 阅读快车系列答案
阅读快车系列答案