题目内容
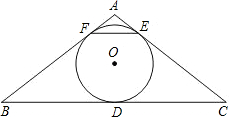
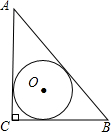
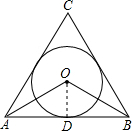
已知等边三角形ABC的边长为2，那么这个三角形的内切圆的半径为______．
过O点作OD⊥AB，
∵O是等边△ABC的内心，
∴∠OAD=30°，
∵等边三角形ABC的边长为2，
∴OA=OB，
∴AD=
AB=1，
∴OD=AD•tan30°=
．
即这个三角形的内切圆的半径为：
．
故答案为：
．
∵O是等边△ABC的内心，
∴∠OAD=30°，
∵等边三角形ABC的边长为2，
∴OA=OB，
∴AD=
| 1 |
| 2 |
∴OD=AD•tan30°=
| ||
| 3 |
即这个三角形的内切圆的半径为：
| ||
| 3 |
故答案为：
| ||
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
