题目内容
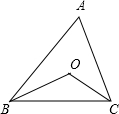
如图，已知⊙O是△ABC的外接圆，CD是AB边上的高，AE是⊙O的直径．求证：AC•BC=AE•CD．
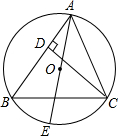
证明：连接EC，
∴∠B=∠E．
∵AE是⊙O的直径，
∴∠ACE=90°．
∵CD是AB边上的高，
∴∠CDB=90°．
在△AEC与△CBD中，
∠E=∠B，∠ACE=∠CDB，
∴△AEC∽△CBD．
∴
=
．
即AC•BC=AE•CD．
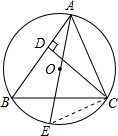
∴∠B=∠E．
∵AE是⊙O的直径，
∴∠ACE=90°．
∵CD是AB边上的高，
∴∠CDB=90°．
在△AEC与△CBD中，
∠E=∠B，∠ACE=∠CDB，
∴△AEC∽△CBD．
∴
| AE |
| BC |
| AC |
| CD |
即AC•BC=AE•CD．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
