ЬтФПФкШн
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§![]() КЭЗДБШР§КЏЪ§
КЭЗДБШР§КЏЪ§![]() ЃЎ
ЃЎ
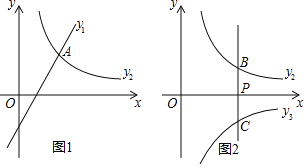
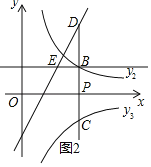
ЃЈ1ЃЉШчЭМ1ЃЌШє![]() ЃЌЧвКЏЪ§
ЃЌЧвКЏЪ§![]() ЁЂ
ЁЂ![]() ЕФЭМЯѓЖМОЙ§Еу
ЕФЭМЯѓЖМОЙ§Еу![]() ЃЎ
ЃЎ
ЂйЧѓ![]() ЃЌ
ЃЌ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкжБНгаДГіЕБ![]() ЪБ
ЪБ![]() ЕФЗЖЮЇЃЛ
ЕФЗЖЮЇЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§Еу![]() зї
зї![]() жсЕФЦНааЯп
жсЕФЦНааЯп![]() гыКЏЪ§
гыКЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕу
ЕФЭМЯѓЯрНЛгкЕу![]() ЃЌгыЗДБШР§КЏЪ§
ЃЌгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕу
ЕФЭМЯѓЯрНЛгкЕу![]() ЃЎ
ЃЎ
ЂйШє![]() ЃЌжБЯп
ЃЌжБЯп![]() гыКЏЪ§
гыКЏЪ§![]() ЕФЭМЯѓЯрНЛЕу
ЕФЭМЯѓЯрНЛЕу![]() ЃЎЕБЕу
ЃЎЕБЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() жаЕФвЛЕуЕНСэЭтСНЕуЕФОрРыЯрЕШЪБЃЌЧѓ
жаЕФвЛЕуЕНСэЭтСНЕуЕФОрРыЯрЕШЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкЙ§Еу![]() зї
зї![]() жсЕФЦНааЯпгыКЏЪ§
жсЕФЦНааЯпгыКЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕу
ЕФЭМЯѓЯрНЛгкЕу![]() ЃЎЕБ
ЃЎЕБ![]() ЕФжЕШЁВЛДѓгк1ЕФШЮвтЪЕЪ§ЪБЃЌЕу
ЕФжЕШЁВЛДѓгк1ЕФШЮвтЪЕЪ§ЪБЃЌЕу![]() ЁЂ
ЁЂ![]() МфЕФОрРыгыЕу
МфЕФОрРыгыЕу![]() ЁЂ
ЁЂ![]() МфЕФОрРыжЎКЭ
МфЕФОрРыжЎКЭ![]() ЪМжеЪЧвЛИіЖЈжЕЃЎЧѓДЫЪБ
ЪМжеЪЧвЛИіЖЈжЕЃЎЧѓДЫЪБ![]() ЕФжЕМАЖЈжЕ
ЕФжЕМАЖЈжЕ![]() ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЌ
ЃЌ![]() ЃЛЂк
ЃЛЂк![]() ЃЛЃЈ2ЃЉЂй
ЃЛЃЈ2ЃЉЂй![]() Лђ4ЃЛЂк
Лђ4ЃЛЂк![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйНЋЕу![]() ЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНМДПЩЧѓНтЃЌНЋЕу
ЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНМДПЩЧѓНтЃЌНЋЕу![]() ЕФзјБъДњШыЗДБШР§КЏЪ§БэДяЪНЃЌМДПЩЧѓНтЃЛЂкгЩЭМЯѓПЩвджБНгПДГіЃЛ
ЕФзјБъДњШыЗДБШР§КЏЪ§БэДяЪНЃЌМДПЩЧѓНтЃЛЂкгЩЭМЯѓПЩвджБНгПДГіЃЛ
ЃЈ2ЃЉЂй![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌгЩ
ЃЌгЩ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЕУЃК
ЕУЃК![]() Лђ0Лђ2ЃЌМДПЩЧѓНтЃЛЂкЕу
Лђ0Лђ2ЃЌМДПЩЧѓНтЃЛЂкЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]()
![]() ЃЌМДПЩЧѓНтЃЎ
ЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉЂйНЋЕу![]() ЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНВЂНтЕУЃК
ЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНВЂНтЕУЃК![]() ЃЌ
ЃЌ
НЋЕу![]() ЕФзјБъДњШыЗДБШР§КЏЪ§ЕУЃК
ЕФзјБъДњШыЗДБШР§КЏЪ§ЕУЃК![]() ЃЛ
ЃЛ
ЂкгЩЭМЯѓПЩвдПДГі![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФзјБъЗжБ№ЮЊ
ЕФзјБъЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дђ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
МДЃК![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
МДЃК![]() Лђ0Лђ2Лђ4ЃЌ
Лђ0Лђ2Лђ4ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гыЬтвтВЛЗћЃЌ
гыЬтвтВЛЗћЃЌ
Еу![]() ВЛФмдк
ВЛФмдк![]() ЕФЯТЗНЃЌМД
ЕФЯТЗНЃЌМД![]() вВВЛДцдкЃЌ
вВВЛДцдкЃЌ![]() ЃЌЙЪ
ЃЌЙЪ![]() ВЛГЩСЂЃЌ
ВЛГЩСЂЃЌ
ЙЪ![]() Лђ4ЃЛ
Лђ4ЃЛ
ЂкЕу![]() ЕФКсзјБъЮЊЃК
ЕФКсзјБъЮЊЃК![]() ЃЌ
ЃЌ
ЕБЕу![]() дкЕу
дкЕу![]() зѓВрЪБЃЌ
зѓВрЪБЃЌ
![]()
![]() ЃЌ
ЃЌ
![]() ЕФжЕШЁВЛДѓгк1ЕФШЮвтЪ§ЪБЃЌ
ЕФжЕШЁВЛДѓгк1ЕФШЮвтЪ§ЪБЃЌ![]() ЪМжеЪЧвЛИіЖЈжЕЃЌ
ЪМжеЪЧвЛИіЖЈжЕЃЌ
ЕБ![]() ЪБЃЌДЫЪБ
ЪБЃЌДЫЪБ![]() ЃЌДгЖј
ЃЌДгЖј![]() ЃЎ
ЃЎ
ЕБЕу![]() дкЕу
дкЕу![]() гвВрЪБЃЌ
гвВрЪБЃЌ
ЭЌРэ![]() ЃЌ
ЃЌ
ЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌЃЈВЛКЯЬтвтЩсШЅЃЉ
ЪБЃЌЃЈВЛКЯЬтвтЩсШЅЃЉ
ЙЪ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ