ƒøƒ⁄»›
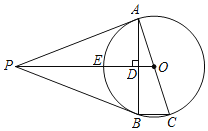
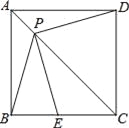
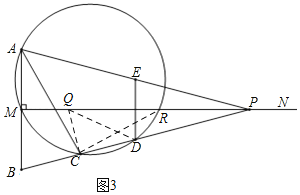
°æƒø°ø»ÁÕº£¨“—÷™œfl∂ŒAB£Ω2£¨MN°ÕAB”⁄µ„M£¨«“AM£ΩBM£¨P «…‰œflMN…œ“ª∂ص„£¨E£¨D∑÷± «PA£¨PBµƒ÷–µ„£¨π˝µ„A£¨M£¨Dµƒ‘≤”ÎBPµƒ¡Ì“ªΩªµ„C(µ„C‘⁄œfl∂ŒBD…œ)£¨”ÎMNµƒ¡Ì“ª∏ˆΩªµ„R£¨¡¨Ω·AC£¨DE£Æ
(1)µ±°œAPB£Ω28°„ ±£¨«Û°œBµƒ∂» ˝∫Õª°CMµƒ∂» ˝£Æ
(2)«Û÷§£∫AC£ΩAB£Æ
(3)»ÙMP=4£¨µ„PŒ™…‰œflMN…œµƒ“ª∏ˆ∂ص„£¨
¢Ÿ«ÛMRµƒ÷µ
¢⁄‘⁄µ„Pµƒ‘À∂Øπ˝≥Ã÷–£¨»°Àƒ±fl–ŒACDE“ª±flµƒ¡Ω∂Àµ„∫Õœfl∂ŒMP…œ“ªµ„Q£¨»Ù“‘’‚»˝µ„Œ™∂•µ„µƒ»˝Ω«–Œ «÷±Ω«»˝Ω«–Œ£¨«“QŒ™»ÒΩ«∂•µ„£¨«Û¥À ±À˘”–¬˙◊„Ãıº˛µƒMQµƒ÷µ£Æ
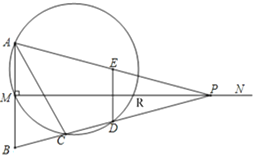
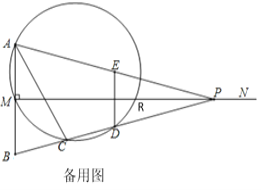
°æ¥∞∏°ø(1)°œB=76°„£¨![]() =56°„£ª(2)÷§√˜º˚Ω‚Œˆ£ª(3)¢ŸMR=
=56°„£ª(2)÷§√˜º˚Ω‚Œˆ£ª(3)¢ŸMR=![]() £ª¢⁄MQµƒ÷µŒ™
£ª¢⁄MQµƒ÷µŒ™![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() .
.
°æΩ‚Œˆ°ø
£®1£©¡¨Ω”MD£¨Ω·∫œ¥π÷±∆Ω∑÷œflµƒ–‘÷ ”ε»—¸»˝Ω«–Œ–‘÷ Ω·∫œ»˝Ω«–Œƒ⁄Ω«∫Õ∂®¿Ì£¨÷–Œªœfl∂®¿Ì«ÛΩ‚º¥ø…£ª
£®2£©«Û÷§°œABC=°œACBº¥ø…£ª
£®3£©¢Ÿ¡¨Ω”CR£¨AR£¨Ω·∫œπ¥π…∂®¿Ì«ÛΩ‚º¥ø…£ª¢⁄∑÷Œ™µ±°œACQ=90°„ ±£ªµ±°œQCD=90°„ ±£ªµ±°œQDC=90°„ ±£ªµ±°œAEQ=90°„ ±£¨∑÷¿‡Ã÷¬€º¥ø…£Æ
Ω‚£∫(1)°flMN°ÕAB£¨AM=BM£¨
°‡PA=PB£¨
°‡°œPAB=°œB£¨
°fl°œAPB=28°„£¨
°‡°œB=76°„£¨
»ÁÕº1£¨¡¨Ω”MD£¨
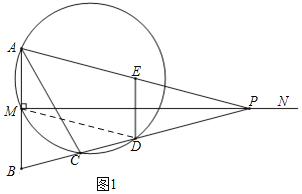
°flMDŒ™°˜PABµƒ÷–Œªœfl£¨
°‡MD°ŒAP£¨
°‡°œMDB=°œAPB=28°„£¨
°‡![]() =2°œMDB=56°„£ª
=2°œMDB=56°„£ª
(2)°fl°œBAC=°œMDC=°œAPB£¨
”÷°fl°œBAP=180°„©Å°œAPB©Å°œB£¨°œACB=180°„©Å°œBAC©Å°œB£¨
°‡°œBAP=°œACB£¨
°fl°œBAP=°œB£¨
°‡°œACB=°œB£¨
°‡AC=AB£ª
(3)¢Ÿ»ÁÕº2£¨º«MP”Α≤µƒ¡Ì“ª∏ˆΩªµ„Œ™R£¨

°flMD «Rt°˜MBPµƒ÷–œfl£¨
°‡DM=DP£¨
°‡°œDPM=°œDMP=°œRCD£¨
°‡RC=RP£¨
°fl°œACR=°œAMR=90°„£¨
°‡AM2+MR2=AR2=AC2+CR2£¨
°‡12+MR2=22+PR2£¨
°‡12+(4©ÅPR)2=22+PR2£¨
°‡PR=![]() £¨
£¨
°‡MR=![]() £¨
£¨
¢⁄¢Ò£Æµ±°œACQ=90°„ ±£¨AQŒ™‘≤µƒ÷±æ∂£¨
°‡Q”ÎR÷ÿ∫œ£¨
°‡MQ=MR=![]() £ª
£ª
¢Ú£Æ»ÁÕº3£¨µ±°œQCD=90°„ ±£¨
‘⁄Rt°˜QCP÷–£¨PQ=2PR=![]() £¨
£¨
°‡MQ=![]() £ª
£ª
¢Û£Æ»ÁÕº4£¨µ±°œQDC=90°„ ±£¨

°flBM=1£¨MP=4£¨
°‡BP=![]() £¨
£¨
°‡DP=![]() BP=
BP=![]() £¨
£¨
°flcos°œMPB=![]()
![]() £¨
£¨
°‡PQ=![]() £¨
£¨
°‡MQ=![]() £ª
£ª
¢Ù£Æ»ÁÕº5£¨µ±°œAEQ=90°„ ±£¨
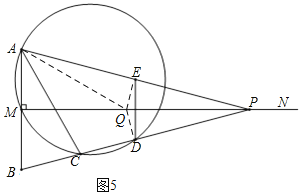
”…∂‘≥∆–‘ø…µ√°œAEQ=°œBDQ=90°„£¨
°‡MQ=![]() £ª
£ª
◊€…œÀ˘ ˆ£¨MQµƒ÷µŒ™![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() .
.

 √˚ ¶∞ȃ„≥…≥§øŒ ±Õ¨≤Ω—ß¡∑≤‚œµ¡–¥∞∏
√˚ ¶∞ȃ„≥…≥§øŒ ±Õ¨≤Ω—ß¡∑≤‚œµ¡–¥∞∏