题目内容
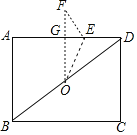
【题目】如图,在矩形ABCD中,AB=6,BC=8,点O为对角线BD的中点,点E为边AD上一点,连接OE,将△DOE沿OE翻折得到△OEF,若OF⊥AD于点G,则OE=______.
【答案】![]()
【解析】
由矩形的性质和勾股定理得出BD=![]() =10,得出OD=5,由折叠的性质得:∠F=∠ADB,OF=OD=5,证出OG是△ABD的中位线,△GEF∽△ABD,得出OG=
=10,得出OD=5,由折叠的性质得:∠F=∠ADB,OF=OD=5,证出OG是△ABD的中位线,△GEF∽△ABD,得出OG=![]() AB=3,
AB=3,![]() =
=![]() ,求出GE=
,求出GE=![]() ,在Rt△OGE中,由勾股定理即可得出结果.
,在Rt△OGE中,由勾股定理即可得出结果.
解:∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=8,
∴AB⊥AD,BD=![]() =10,
=10,
∵点O为对角线BD的中点,
∴OD=5,
由折叠的性质得:∠F=∠ADB,OF=OD=5,
∵OF⊥AD,∴OF∥AB,∠OGE=∠FGE=90°=∠A,
∴OG是△ABD的中位线,△GEF∽△ABD,
∴OG=![]() AB=3,
AB=3,![]() =
=![]() ,
,
∴FG=OF-OG=2,![]() =
=![]() ,
,
∴GE=![]() ,
,
在Rt△OGE中,由勾股定理得:OE=![]() =
=![]() =
=![]() ;
;
故答案是:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目