题目内容
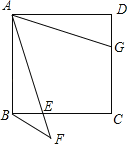
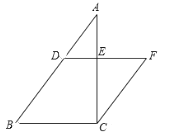
【题目】如图，在Rt△ABC中，∠ACB = 90°，BC = 6，AC = 8．点D是AB边上一点，过点D作DE // BC，交边AC于E．过点C作CF // AB，交DE的延长线于点F．
（1）如果
，求线段EF的长；
（2）求∠CFE的正弦值．
【答案】（1）4；（2）
.
【解析】
（1）根据相似三角形的性质得到 
，求得DE=2，推出四边形BCFD是平行四边形，根据平行四边形的性质得到DF=BC=6，于是得到结论；
（2）根据平行四边形的性质得到∠B=∠F，根据勾股定理得
，根据三角函数的定义即可得到结论．
解：（1）∵ DE // BC，∴ ．
又∵ BC = 6，∴ DE = 2．
∵ DF // BC，CF // AB，∴ 四边形BCFD是平行四边形．
∴ DF = BC = 6．∴ EF = DF – DE = 4．
（2）∵ 四边形BCFD是平行四边形， ∴ ∠B =∠F．
在Rt△ABC中，∠ACB = 90°，BC = 6，AC = 8，
利用勾股定理，得
．
∴ 
．∴ 
．
练习册系列答案
相关题目
