题目内容
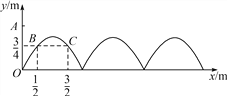
【题目】如图，需在一面墙上绘制几个相同的抛物线型图案．按照图中的直角坐标系，最左边的抛物线可以用y＝ax2＋bx(a≠0)表示．已知抛物线上B，C两点到地面的距离均为
m，到墙边OA的距离分别为
m，
m.
(1)求该拋物线的函数关系式，并求图案最高点到地面的距离；
(2)若该墙的长度为10 m，则最多可以连续绘制几个这样的拋物线型图案？
【答案】（1）1；（2）最多可以连续绘制5个这样的拋物线型图案．
【解析】试题分析：（1）根据题意求得B（
，
），C（
，），解方程组求得拋物线的函数关系式为y=-x2+2x；根据抛物线的顶点坐标公式得到结果；
（2）令y=0，即-x2+2x=0，解方程得到x1=0，x2=2，即可得到结论．
试题解析：（1）根据题意得：B（，），C（，），
把B，C代入y=ax2+bx得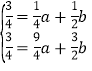
，
解得：
，
∴拋物线的函数关系式为y=﹣x2+2x；
∴图案最高点到地面的距离=
；
（2）令y=0，即﹣x2+2x=0，
∴x1=0，x2=2，
∴10÷2=5，
∴最多可以连续绘制5个这样的拋物线型图案．
练习册系列答案
相关题目
