题目内容
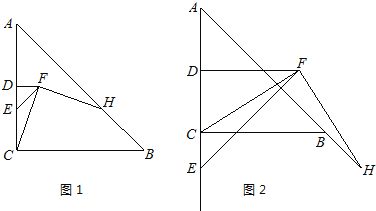
【题目】如图，等腰△ABC中，CA=CB=6，AB=6
．点D在线段AB上运动（不与A、B重合），将△CAD与△CBD分别沿直线CA、CB翻折得到△CAE与△CBF，连接EF，则△CEF面积的最小值为_____．
【答案】
【解析】
作CH⊥AB于H．首先证明△ECF是顶角为120°的等腰三角形，根据此线段最短可知CD的最小值为3，延长即可解决问题.
解：作CH⊥AB于H．
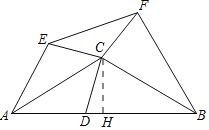
∵CA=CB，CH⊥AB，
∴AH=BH=3
，
∴cos∠CAH=
=
，
∴∠CAB=∠CBA=30°，
∴∠ACB=120°，CH=
AC=3，
由翻折不变性可知：CD=CE=CF，∠ACE=∠ACD，∠BCD=∠BCF，
∴∠ECF=360°-120°-120°=120°，
∴△ECF是顶角为120°的等腰三角形，
∴当CE的长最短时，△ECF的面积最小，
根据垂线段最短可知，当CD与CH重合时，EC=CD=CH=3，
∴S△ECF=×3×
=，
故答案为:．
练习册系列答案
相关题目
