Question

【题目】在 中，，点 为的中点．
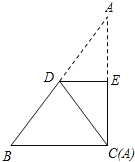
（1）如图1，E为线段DC上任意一点，将线段绕点D逆时针旋转90°得到线段，连接 ，过点F作，交直线 于点 ．判断 与的数量关系并加以证明；
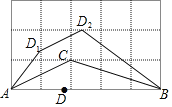
（2）如图2，若为线段的延长线上任意一点，（1）中的其他条件不变，你在（1）中得出的结论是否发生改变，直接写出你的结论，不必证明．

Answer 1

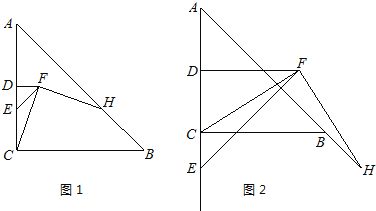
【答案】（1）FH=FC．理由见解析；（2）FH与FC仍然相等．理由见解析

【解析】

（1）延长DF交AB于点G，根据三角形中位线的判定得出点G为AB的中点，根据中位线的性质及已知条件AC=BC，得出DC=DG，从而EC=FG，易证∠1=∠2=90°-∠DFC，∠CEF=∠FGH=135°，由AAS证出△CEF≌△FGH．∴CF=FH．
（2）通过证明△CEF≌△FGH（ASA）得出．

（1）FH与FC的数量关系是：FH=FC．
证明如下：延长DF交AB于点G，

由题意，知∠EDF=∠ACB=90°，DE=DF，
∴DG∥CB，
∵点D为AC的中点，
∴点G为AB的中点，且DC＝AC，
∴DG为△ABC的中位线，
∴DG＝BC．
∵AC=BC，
∴DC=DG，
∴DC-DE=DG-DF，
即EC=FG．
∵∠EDF=90°，FH⊥FC，
∴∠1+∠CFD=90°，∠2+∠CFD=90°，
∴∠1=∠2．
∵△DEF与△ADG都是等腰直角三角形，
∴∠DEF=∠DGA=45°，
∴∠CEF=∠FGH=135°，
∴△CEF≌△FGH，
∴CF=FH．
（2）FH与FC仍然相等．

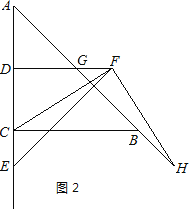
理由：由题意可得出：DF=DE，
∴∠DFE=∠DEF=45°，
∵AC=BC，
∴∠A=∠CBA=45°，
∵DF∥BC，
∴∠CBA=∠FGB=45°，
∴∠FGH=∠CEF=45°，
∵点D为AC的中点，DF∥BC，
∴DG=BC，DC=AC，
∴DG=DC，
∴EC=GF，
∵∠DFC=∠FCB，
∴∠GFH=∠FCE，
在△FCE和△HFG中
，
∴△FCE≌△HFG（ASA），
∴HF=FC．