题目内容
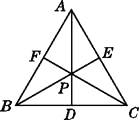
【题目】如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是_____.

【答案】2![]() .
.
【解析】求出∠ACB,根据线段垂直平分线求出AD=CD,求出∠ACD、∠DCB,求出CD、AD、AB,由勾股定理求出BC,再求出AC即可.
解:∵∠A=30°,∠B=90°,
∴∠ACB=180°﹣30°﹣90°=60°,
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠A=∠ACD=30°,
∴∠DCB=60°﹣30°=30°,
∵BD=1,
∴CD=AD=2,
∴AB=1+2=3,
在Rt△BCD中,由勾股定理得:CB=![]() ,
,
在Rt△ABC中,由勾股定理得:AC=![]() =2
=2![]() ,
,
故答案为:2![]() .
.
“点睛”本题考查了线段垂直平分线,含30度角的直角三角形,等腰三角形的性质,三角形的内角和定理等知识点的应用,主要考查学生运用这些定理进行推理的能力,题目综合性比较强,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目