Question

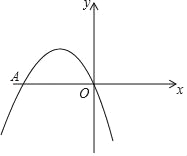
【题目】如图，二次函数y=ax2﹣4x+c的图象经过坐标原点，与x轴交于点A（﹣4，0）．

（1）该二次函数的关系式是　 　，顶点坐标　 　．

（2）根据图象回答：当x满足　 　时，y＞0；

（3）在抛物线上存在点P，满足S△AOP=8，请直接写出点P的坐标　 　．

Answer 1

【答案】（1）y=﹣x2﹣4x或y=﹣（x+2）2+4，（﹣2，4）；（2）﹣4＜x＜0；（3）（﹣2，4）、（﹣2+2，﹣4）、（﹣2﹣2，﹣4）

【解析】

（1）把点A原点的坐标代入函数解析式，利用待定系数法求二次函数解析式解答；

（2）直接利用函数图象得出不等式ax2﹣4x+c＞0的解集；

（3）根据三角形的面积公式求出点P到AO的距离，然后分点P在x轴的上方与下方两种情况解答即可．

解：（1）由已知条件得：

，

解得：，

所以，此二次函数的解析式为：y=﹣x2﹣4x或y=﹣（x+2）2+4，

故顶点坐标是（﹣2，4）．

故答案是：y=﹣x2﹣4x或y=﹣（x+2）2+4；（﹣2，4）．

（2）如图所示：当﹣4＜x＜0时，y＞0．

故答案是：﹣4＜x＜0；

（3）∵点A的坐标为（﹣4，0），

∴AO=4，

设点P到x轴的距离为h，

则S△AOP=×4h=8，

解得h=4，

①当点P在x轴上方时，﹣x2﹣4x=4，

解得：x=﹣2，

所以，点P的坐标为（﹣2，4），

②当点P在x轴下方时，﹣x2﹣4x=﹣4，

解得x1=﹣2+2，x2=﹣2﹣2，

所以，点P的坐标为（﹣2+2，﹣4）或（﹣2﹣2，﹣4），

综上所述，点P的坐标是：（﹣2，4）、（﹣2+2，﹣4）、（﹣2﹣2，﹣4）．

故答案是：（﹣2，4）、（﹣2+2，﹣4）、（﹣2﹣2，﹣4）．