Question

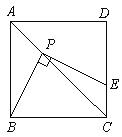
【题目】如图，正方形ABCD的边长为6，P为对角线AC上一点，且CP=，PE⊥PB交CD于点E，则PE=（ ）

A.B.C.D.5

Answer 1

【答案】B

【解析】

过P作PM⊥BC于M，作PN⊥CD于N，易证△PBM≌△PEN，从而PB=PE，在Rt△PBM中求出BM、PM即可用勾股定理求解．

过P作PM⊥BC于M，作PN⊥CD于N，

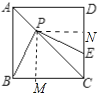
∵四边形ABCD是正方形

∴∠BMP=∠PMC=∠MCN=∠CNP=90°，CA平分∠BCD

∴PM=PN，∠MPN=90°

∵PE⊥PB

∴∠BPM+∠MPC=90°，∠MPC+∠EPN=90°

∴∠BPM=∠EPN

∴△PBM≌△PEN

∴PB=PE，
在Rt△PCM中，CP=4，∠PCM=45°

∴CM=PM=4
∴BM=BC-CM=2
在Rt△PBM中，PM=4，BM=2
∴PB=

∴PE=PB=
故选：B