Question

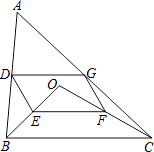
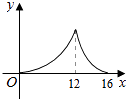
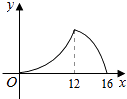
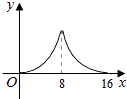
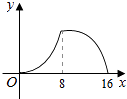
【题目】已知：如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F；当直线EF停止运动时，点P也停止运动．连接PF，设运动时间为t（s）（0＜t＜8）．设四边形APFE的面积为y（cm2），则下列图象中，能表示y与t的函数关系的图象大致是（ ）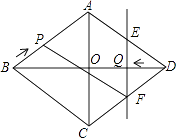

A.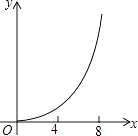
B.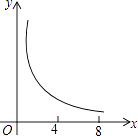
C.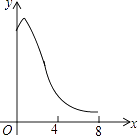
D.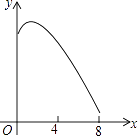

Answer 1

【答案】D
【解析】解：如图，过点C作CG⊥AB于点G，
∵S菱形ABCD=ABCG= ACBD，
即10CG= ×12×16，
∴CG= ．
∴S梯形APFD= （AP+DF）CG
= （10﹣t+ t） = t+48．
∵△DFQ∽△DCO，
∴ = ，
即 = ，
∴QF= t．
同理，EQ= t．
∴EF=QF+EQ= t．
∴S△EFD= EFQD= × t×t= t2 ．
∴y=（ t+48）﹣ t2=﹣ t2+ t+48．
是二次函数，开口向下，D答案符合，
故选D．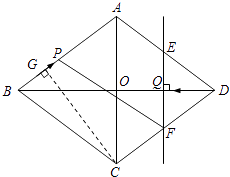

过点C作CG⊥AB于点G，由S菱形ABCD=ABCG= ACBD，求出CG．据S梯形APFD= （AP+DF）CG．S△EFD= EFQD．得出y与t之间的函数关系式；