题目内容
【题目】如图，以AB为直径的⊙O与弦CD相交于点E，且AC=2，AE= 
，CE=1．则 
的长是（ ）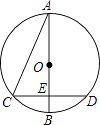 
A.
B.
C.
D.
【答案】B
【解析】解：连接OC， ∵△ACE中，AC=2，AE= 
，CE=1，
∴AE2+CE2=AC2 ，
∴△ACE是直角三角形，即AE⊥CD，
∵sinA= 
= 
，
∴∠A=30°，
∴∠COE=60°，
∴ 
=sin∠COE，即 
= 
，解得OC= 
，
∵AE⊥CD，
∴ 
= 
，
∴ = = 
= 
．
故选：B．
连接OC，先根据勾股定理判断出△ACE的形状，再由垂径定理得出CE=DE，故 = ，由锐角三角函数的定义求出∠A的度数，故可得出∠BOC的度数，求出OC的长，再根据弧长公式即可得出结论．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】某中学九年级1班同学积极响应“阳光体育工程”的号召，利用课外活动时间积极参加体育锻炼，每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练，训练前后都进行了测试．现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表．
进球数（个） | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
训练后篮球定时定点投篮测试进球数统计表
请你根据图表中的信息回答下列问题：
（1）选择长跑训练的人数占全班人数的百分比为 ， 该班学生的总人数为；
（2）训练后篮球定时定点投篮人均进球数为；
（3）若将选择篮球的同学的进球数写在外观、大小一样的枝条上，放在不透明的盒子中，搅拌均匀后，从中抽取一张，则抽到4的概率是多少？
