题目内容
【题目】在矩形ABCD中,AD=5,AB=4,点E,F在直线AD上,且四边形BCFE为菱形.若线段EF的中点为点M,则线段AM的长为 .
【答案】5.5,或0.5
【解析】解:分两种情况:①如图1所示: 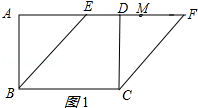
∵四边形ABCD是矩形,
∴CD=AB=4,BC=AD=5,∠ADC=∠CDF=90°,
∵四边形BCFE为菱形,
∴CF=EF=BE=BC=5,
∴DF= ![]() =
= ![]() =3,
=3,
∴AF=AD+DF=8,
∵M是EF的中点,
∴MF= ![]() EF=2.5,
EF=2.5,
∴AM=AF﹣DF=8﹣2.5=5.5;
②如图2所示:同①得:AE=3,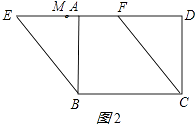
∵M是EF的中点,
∴ME=2.5,
∴AM=AE﹣ME=0.5;
综上所述:线段AM的长为:5.5,或0.5;
故答案为:5.5,或0.5.
两种情况:①由矩形的性质得出CD=AB=4,BC=AD=5,∠ADB=∠CDF=90°,由菱形的性质得出CF=EF=BE=BC=5,由勾股定理求出DF,得出MF,即可求出AM;②同①得出AE=3,求出ME,即可得出AM的长.

练习册系列答案
相关题目