题目内容
【题目】综合与实践
问题情境
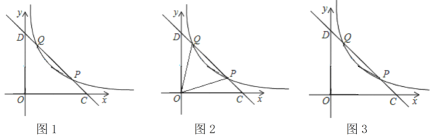
在综合与实践课上,老师让同学们以“大小不等的两个正方形”为主题开展数学活动,如图1,现有一个边长为![]() 的正方形
的正方形![]() ,点
,点![]() 从对角线
从对角线![]() 的点
的点![]() 出发向点
出发向点![]() 运动,连接
运动,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,以
,以![]() 为边在
为边在![]() 右侧作正方形
右侧作正方形![]() ,边
,边![]() 与射线
与射线![]() 交于点
交于点![]() .
.
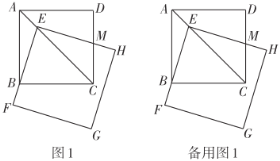
操作发现
(1)点![]() 在运动过程中,判断线段
在运动过程中,判断线段![]() 与线段
与线段![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
实践探究
(2)在点![]() 的运动过程中,某时刻正方形
的运动过程中,某时刻正方形![]() 与正方形
与正方形![]() 重叠的四边形
重叠的四边形![]() 的面积是
的面积是![]() ,求此时
,求此时![]() 的长;
的长;
探究拓广
(3)请借助备用图2,探究当点![]() 不与点
不与点![]() ,
,![]() 重合时,线段
重合时,线段![]() ,
,![]() 与
与![]() 之间存在的数量关系,请直接写出.
之间存在的数量关系,请直接写出.
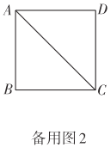
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ;(3)①当
;(3)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() 且点
且点![]() 与点
与点![]() 重合;③当
重合;③当![]() 时,
时,![]()
【解析】
(1)首先由正方形的性质得出![]() ,
,![]() ,
,![]() ,然后判定
,然后判定![]() ,进而得出
,进而得出![]() ,
,![]() ,又由正方形EFGH得出
,又由正方形EFGH得出![]() ,再由四边形内角和得出
,再由四边形内角和得出![]() ,进而得出
,进而得出![]() ,
,![]() ;
;
(2)首先过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,得出
,得出![]() ,然后由对角线的性质得出
,然后由对角线的性质得出![]() ,
,![]() ,进而判定四边形
,进而判定四边形![]() 是正方形,即可判定
是正方形,即可判定![]() ,然后通过面积的等量代换得出CE,进而得出AE.
,然后通过面积的等量代换得出CE,进而得出AE.
(3)根据题意,分三种情况讨论即可:①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时.
时.
(1)![]() .
.
理由如下:如图,连接![]() .
.
∵![]() 是正方形
是正方形![]() 的对角线,
的对角线,
∴![]() ,
,![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,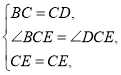
∴![]() .
.
∴![]() ,
,![]() .
.
∵四边形![]() 是正方形,
是正方形,
∴![]() .
.
在四边形![]() 中,
中,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
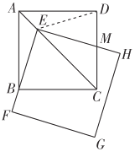
(2)如图,过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() .
.
∴![]() .
.
∵点![]() 是正方形
是正方形![]() 的对角线
的对角线![]() 上的点,
上的点,
∴![]() ,
,![]() .
.
∴四边形![]() 是正方形.
是正方形.
在![]() 和
和![]() 中,
中,
![]()
∴![]() .
.
∴![]() .
.
∴![]()
![]() .
.
∵正方形![]() 与正方形
与正方形![]() 重叠的面积是
重叠的面积是![]() ,
,
∴![]() .解得
.解得![]() .
.
∵正方形![]() 的边长为6,
的边长为6,
∴![]() .
.
∴![]() .
.
∴此时![]() 的长为
的长为![]() .
.
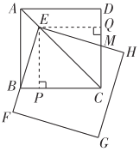
(3)分三种情况:
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() 且点
且点![]() 与点
与点![]() 重合;
重合;
③当![]() 时,
时,![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某厂按用户需求生产一种产品,成本每件20万元,规定每件售价不低于成本,且不高于40万元。经市场调查,每年的销售量y(件)与每件售价x(万元)满足一次函数关系,部分数据如下表:
售价x(万元/件) | 25 | 30 | 35 |
销售量y(件) | 50 | 40 | 30 |
(1)求y与x之间的函数表达式;
(2)设商品每年的总利润为W(万元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少万元时获得最大利润,最大利润是多少?