题目内容
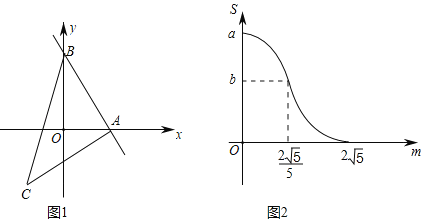
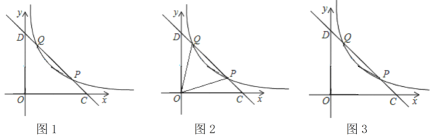
【题目】如图1,在平面直角坐标系xOy中,函数![]() (m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点.
(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点.
(1)求∠OCD的度数;
(2)如图2,连接OQ、OP,当∠DOQ=∠OCD-∠POC时,求此时m的值;
(3)如图3,点A,点B分别在x轴和y轴正半轴上的动点.再以OA、OB为邻边作矩形OAMB.若点M恰好在函数![]() (m为常数,m>1,x>0)的图象上,且四边形BAPQ为平行四边形,求此时OA、OB的长度.
(m为常数,m>1,x>0)的图象上,且四边形BAPQ为平行四边形,求此时OA、OB的长度.
【答案】(1)45°;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由点坐标可得点D、C的坐标,可得OC,OD的长,证明![]() 为等腰直角三角形,所以∠OCD的度数为45°;(2)因为
为等腰直角三角形,所以∠OCD的度数为45°;(2)因为![]() ,所以
,所以![]() ,即∠QOP=45°,由勾股定理得,
,即∠QOP=45°,由勾股定理得,![]() ,
,![]() ,解得
,解得![]() ;(3)由四边形ABPQ为平行四边形,可得
;(3)由四边形ABPQ为平行四边形,可得![]() ,即
,即![]() ,所以OA=OB,设OA=OB=n,则M为(n,n)代入
,所以OA=OB,设OA=OB=n,则M为(n,n)代入![]() ,得
,得![]() ,所以
,所以![]() ,根据AB=PQ列式得,
,根据AB=PQ列式得,![]() ,由①②得,
,由①②得,![]() ,即当OA=OB=
,即当OA=OB=![]() 时,符合题意;
时,符合题意;
解:

(2)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
易得![]() ,
,
∴![]() ,
,
解得![]() ;
;
(3)∵四边形ABPQ为平行四边形,
∴![]() ,
,
∴![]() ,
,
∴OA=OB,
设OA=OB=n,
则M为(n,n)代入![]() ,
,
∴![]() ,
,
∴![]() ,
,
又AB=PQ,
∴![]() ,
,
由①②得,![]() ;
;
∴当OA=OB=![]() 时,符合题意;
时,符合题意;


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目