题目内容
【题目】如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,以A为圆心、AB为半径画圆,与边BC交于另一点D.
,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.

【答案】(1)BD=2;(2)sin∠DAC=![]() .
.
【解析】
(1)如图连接AD,作AH⊥BD于H.利用面积法求出AH,再利用勾股定理求出BH即可解决问题;
(2)作DM⊥AC于M.利用面积法求出DM即可解决问题.
(1)如图连接AD,作AH⊥BD于H.
∵Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,∴AB
,∴AB![]()
![]() ABAC
ABAC![]() BCAH,∴AH
BCAH,∴AH![]() 2,∴BH
2,∴BH![]() 1.
1.
∵AB=AD,AH⊥BD,∴BH=HD=1,∴BD=2.
(2)作DM⊥AC于M.
∵S△ACB=S△ABD+S△ACD,∴![]() 2×2
2×2![]() DM,∴DM
DM,∴DM![]() ,∴sin∠DAC
,∴sin∠DAC![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
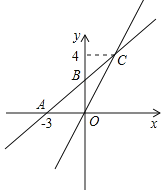
【题目】抛物线y=ax2+bx+c(a≠0,a、b、c为常数)上部分点的横坐标x,纵坐标y的对应值如下表:
x | …… | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
| 4 |
| 4 | m | 0 | …… |
则下列结论中:①抛物线的对称轴为直线x=﹣1;②m=![]() ;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
A.1个B.2个C.3个D.4个