Question

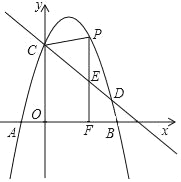
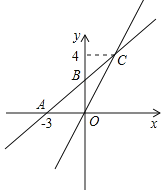
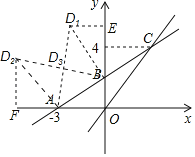
【题目】如图，在平面直角坐标系中，一次函数y＝kx+b的图象与x轴交于点A（﹣3，0），与y轴交于点B，且与正比例函数y＝x的图象交点为C（m，4）．

（1）求一次函数y＝kx+b的解析式；

（2）求△BOC的面积；

（3）若点D在第二象限，△DAB为等腰直角三角形，则点D的坐标为　 　．

Answer 1

【答案】（1）y＝x+2；（2）3；（3）（﹣2，5）或（﹣5，3）或（，）．

【解析】

（1）把C点坐标代入正比例函数解析式可求得m，再把A、C坐标代入一次函数解析式可求得k、b，可求得答案；

（2）先求出点B的坐标，然后根据三角形的面积公式即可得到结论；

（3）由题意可分AB为直角边和AB为斜边两种情况，当AB为直角边时，再分A为直角顶点和B为直角顶点两种情况，此时分别设对应的D点为D2和D1，过点D1作D1E⊥y轴于点E，过点D2作D2F⊥x轴于点F，可证明△BED1≌△AOB（AAS），可求得D1的坐标，同理可求得D2的坐标，AD1与BD2的交点D3就是AB为斜边时的直角顶点，据此即可得出D点的坐标．

（1）∵点C（m，4）在正比例函数y＝x的图象上，

∴m＝4，

解得：m＝3，

∴C（3，4），

∵点C（3，4）、A（﹣3，0）在一次函数y＝kx+b的图象上，

∴，

解得，

∴一次函数的解析式为y＝x+2；

（2）在y＝x+2中，令x＝0，解得y＝2，

∴B（0，2），

∴S△BOC＝×2×3＝3；

（3）分AB为直角边和AB为斜边两种情况，

当AB为直角边时，分A为直角顶点和B为直角顶点两种情况，

如图，过点D1作D1E⊥y轴于点E，过点D2作D2F⊥x轴于点F，

∵点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，

∴AB＝BD1，

∵∠D1BE+∠ABO＝90°，∠ABO+∠BAO＝90°，

∴∠BAO＝∠EBD1，

∵在△BED1和△AOB中，

，

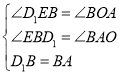∴△BED1≌△AOB（AAS），

∴BE＝AO＝3，D1E＝BO＝2，

∴OE=OB+BE=2+3=5，

∴点D1的坐标为（﹣2，5）；

同理可得出：△AFD2≌△AOB，

∴FA＝BO＝2，D2F＝AO＝3，

∴点D2的坐标为（﹣5，3），

当AB为斜边时，如图，

∵∠D1AB＝∠D2BA＝45°，

∴∠AD3B＝90°，

设AD1的解析式为y=k1x+b1，

将A（-3，0）、D1（-2，5）代入得，

解得：，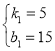

所以AD1的解析式为：y=5x+15，

设BD2的解析式为y=k2x+b2，

将B（0，2）、D2（-5，3）代入得，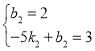

解得：，

所以AD2的解析式为：y=x+2，

解方程组得：，

∴D3（，），

综上可知点D的坐标为（﹣2，5）或（﹣5，3）或（，）．

故答案为：（﹣2，5）或（﹣5，3）或（，）．