题目内容
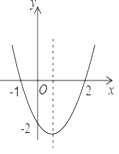
【题目】抛物线y=ax2+bx+c(a≠0,a、b、c为常数)上部分点的横坐标x,纵坐标y的对应值如下表:
x | …… | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
| 4 |
| 4 | m | 0 | …… |
则下列结论中:①抛物线的对称轴为直线x=﹣1;②m=![]() ;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①根据表格中x与y的对应值和函数的对称性,可得出函数的对称轴;
②函数的对称轴为:x=-1,则m和![]() 对应,即可求解;
对应,即可求解;
③当x=2时y=0,根据函数的对称性,x=-4,y=0,而当-4<x<2时,y>0,即可求解;
④方程ax2+bx+c-4=0的两根,就是y=ax2+bx+c和y=4的两图像的交点的横坐标,即可求解.
解:①根据表格可得,函数的对称轴为:x=-1,此时y=![]() ,故①符合题意;
,故①符合题意;
②函数的对称轴为:x=-1,则m和![]() 对应,故②符合题意;
对应,故②符合题意;
③∵x=2,y=0,∴根据函数的对称性,x=-4,y=0,∴当-4<x<2时,y>0,故③不符合题意;
④∵ax2+bx+c-4=0,∴ax2+bx+c=4∴方程ax2+bx+c-4=0的两根,就是y=ax2+bx+c和y=4的两图像的交点的横坐标∴x1=﹣2,x2=0,故④符合题意,
故选:C.

练习册系列答案
相关题目