题目内容
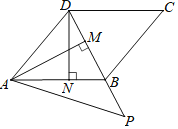
【题目】如图,已知在△ABC中,AB=AC=6,BC=5,D是AB上一点,BD=2,E是BC上一动点,联结DE,并作∠DEF=∠B,射线EF交线段AC于F.
(1)求证:△DBE∽△ECF;
(2)当F是线段AC中点时,求线段BE的长;
(3)联结DF,如果△DEF与△DBE相似,求FC的长.
【答案】(1)见解析;(2)2或3;(3)2或![]()
【解析】
(1)根据等腰三角形的性质得到∠B=∠C,由三角形的内角和和平角的定义得到∠DEF=∠B,根据相似三角形的判定定理即可得到结论;
(2)根据相似三角形的性质得到结论;
(3)当∠BED=∠EDF,得到DF∥BC,根据平行线的性质得到∠ADF=∠B,∠AFD=∠C,根据等腰三角形的性质得到CF=2;当∠DFE=∠BED,推出点E在∠BDF与∠DFC的角平分线上,过E 作EM⊥AB于M,EN⊥AC于N,EG⊥DF于G,连接AE,得到AE是∠BAC的角平分线,根据相似三角形的性质即可得到结论.
(1)∵AB=AC=6,
∴∠B=∠C,
∵∠BDE=180°﹣∠B﹣∠BED,∠CEF=180°﹣∠DEF﹣∠BED,
∵∠DEF=∠B,
∴∠BDE=∠CEF,
∴△DBE∽△ECF;
(2)∵△DBE∽△ECF,
∴![]() ,
,
∵F是线段AC中点,
∴CF=![]() AC=3,
AC=3,
∴![]() ,
,
∴BE=2或3;
(3)∵△DEF与△DBE相似,
∴∠BED=∠EDF,或∠DFE=∠BED,
当∠BED=∠EDF,
∴DF∥BC,
∴∠ADF=∠B,∠AFD=∠C,
∴∠ADF=∠AFD,
∴AD=AF=4,
∴CF=2;
当∠DFE=∠BED,
∵△DBE∽△ECF,
∴∠BED=∠CFE,
∴∠DFE=∠CFE,∠BDE=∠FDE,
∴点E在∠BDF与∠DFC的角平分线上,
过E 作EM⊥AB于M,EN⊥AC于N,EG⊥DF于G,连接AE,
∴EM=EG=EN,
∴AE是∠BAC的角平分线,
∴BE=CE=![]() ,
,
∵△DBE∽△ECF,
∴![]() ,
,
即![]() =
=![]() ,
,
∴CF=![]() .
.
综上所述,FC的长为2或![]() .
.

 名校课堂系列答案
名校课堂系列答案