题目内容
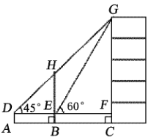
【题目】如图,某数学兴趣小组为测量一棵古树BH和教学楼![]() 的高,先在点
的高,先在点![]() 处用高1.5米的测角仪测得古树顶端点
处用高1.5米的测角仪测得古树顶端点![]() 的仰角
的仰角![]() 为
为![]() ,此时教学楼顶端点
,此时教学楼顶端点![]() 恰好在视线
恰好在视线![]() 上,再向前走7米到达点
上,再向前走7米到达点![]() 处,又测得教学楼顶端点
处,又测得教学楼顶端点![]() 的仰角
的仰角![]() 为
为![]() ,点
,点![]() 、
、![]() 、
、![]() 点在同一水平线上.
点在同一水平线上.
(1)计算古树![]() 的高度;
的高度;
(2)计算教学楼![]() 的高度.(结果精确到0.1米,参考数据:
的高度.(结果精确到0.1米,参考数据:![]() ,
,![]() ).
).
【答案】(1)8.5米;(2)18.0米
【解析】
(1)先根据题意得出DE=AB=7米,AD=BE=1.5米,在Rt△DEH中,可求出HE的长度,进而可计算古树![]() 的高度;
的高度;
(2)作HJ⊥CG于G,设HJ=GJ=BC=x,在Rt△EFG中,利用特殊角的三角函数值求出x的值,进而求出GF,最后利用 CG=CF+FG即可得出答案.
解:(1)由题意:四边形ABED是矩形,可得DE=AB=7米,AD=BE=1.5米,
在Rt△DEH中,
∵∠EDH=45°,
∴HE=DE=7米.
∴BH=EH+BE=8.5米.
答:古树BH的高度为8.5米.
(2)作HJ⊥CG于G.则△HJG是等腰直角三角形,四边形BCJH是矩形,设HJ=GJ=BC=x.
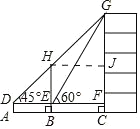
在Rt△EFG中,tan60°=![]() ,
,
∴![]() ,
,
∴GF=![]() ≈16.45
≈16.45
∴CG=CF+FG=1.5+16.45≈17.95≈18.0米.
答:教学楼CG的高度为18.0米.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目