��Ŀ����
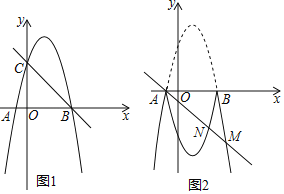
����Ŀ����֪һ�κ���![]() ��ͼ����
��ͼ����![]() ���
���![]() ��ֱ���
��ֱ���![]() ��
��![]() ���㣬�뷴��������
���㣬�뷴��������![]() ��ͼ��ֱ���
��ͼ��ֱ���![]() ��
��![]() ���㣮
���㣮
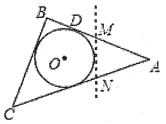
��1����ͼ����![]() ����
����![]() ���߶�
���߶�![]() �ϣ������
�ϣ������![]() ��
��![]() �غϣ�ʱ������
�غϣ�ʱ������![]() ��
��![]() ���
���![]() ��Ĵ��ߣ�����Ϊ
��Ĵ��ߣ�����Ϊ![]() ��
��![]() ��������
��������![]() �����Ϊ2ʱ�������
�����Ϊ2ʱ�������![]() ��λ�ã�
��λ�ã�
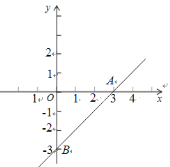
��2����ͼ����![]() ʱ����
ʱ����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ������ڣ������
���ƣ������ڣ������![]() �����ꣻ�������ڣ�˵�����ɣ�
�����ꣻ�������ڣ�˵�����ɣ�
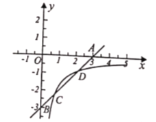
��3����ij�����������ε�һ���߳�Ϊ5���������߳�ǡ������������ͼ��Ľ�������꣬��![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ��
��![]() ����2�����ڣ�
����2�����ڣ�![]() ��
��![]() ����3��
����3��![]()
��������
��1��������֪�����������������ʽ��Ȼ�����ƽ�еõ�![]() ���ó�
���ó�![]() ���ֽ�Ͼ������=
���ֽ�Ͼ������=![]() ������������
������������
��2��������֪�����Ƶ�����E��A����࣬Ȼ�����C,D�������꣬�ٷ���������������ٵ�![]() ���ڵ�
���ڵ�![]() ���ó�
���ó�![]() �������ɵó������
�������ɵó������
��3������һ�κ����ͷ����������Ľ���ʽ�ó������飬��ȥy�ó�����x��һԪ���η��̣����x��ֵ���ٷ��������������������ε����߹�ϵ��⣺��5Ϊ���������ε�������
��5Ϊ���������εױ߳�.�����ó�k��ֵ.
�⣺��1����![]() ʱ��
ʱ��![]() ��
��
��ͼ����![]() �ᣬ
�ᣬ![]() �ᣬ��
�ᣬ��![]() ��
��
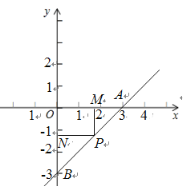
��![]() ����
����![]() �٣�
�٣�
���������Ϊ2����![]() ��.
��.
���ɢ٢ڵ�![]() Ϊ1��2.
Ϊ1��2.
��![]() ��
��![]() .
.
��2����![]() ����
����![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() �㲻������
�㲻������![]() ���Ҳ࣬
���Ҳ࣬
��![]() ��
��![]() �����ʱ��
�����ʱ��![]() ��
��![]()
����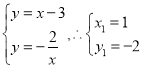 ��
��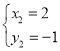
��![]() ��
��![]() .
.
�ٵ�![]() ����
����![]() .
.
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() .
.
��![]() .
.
�ڵ�![]() ����
����![]() ��
��
��![]() ����
����![]() .
.
����������![]() ��
��![]() .
.
��3����![]() ��
��![]() ʱ��
ʱ��
����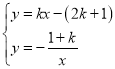 ��
��
��![]() ��
��
![]() ��
��
![]() ��
��![]() .
.
�ٵ�5Ϊ���������ε�����ʱ��![]() .
.
�ڵ�5Ϊ���������εױ߳�ʱ��![]() ��
��
��![]() ������ȥ.
������ȥ.
��ˣ����ϣ�![]() .
.