题目内容
【题目】请用学过的方法研究一类新函数![]() (
(![]() 为常数,
为常数,![]() )的图象和性质.
)的图象和性质.
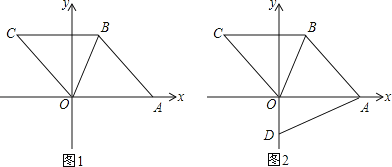
(1)在给出的平面直角坐标系中画出函数![]() 的图象;
的图象;
(2)对于函数![]() ,当自变量
,当自变量![]() 的值增大时,函数值
的值增大时,函数值![]() 怎样变化?
怎样变化?
【答案】解:(1)画图像见解析;(2)①k>0时,当x<0,y随x增大而增大,x>0时,y随x增大而减小;②k<0时,当x<0,y随x增大而减小,x>0时,y随x增大而增大.
【解析】
(1)分两种情况,当x>0时,![]() ,当x<0时,
,当x<0时,![]() ,进而即可画出函数图象;
,进而即可画出函数图象;
(2)分两种情况k>0时,k<0时,分别写出函数![]() 的增减性,即可.
的增减性,即可.
∵当x>0时,![]() ,当x<0时,
,当x<0时,![]() ,
,
∴函数![]() 的图象,如图所示:
的图象,如图所示:
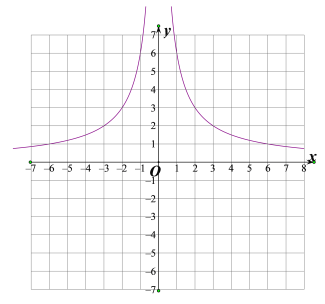
(2)①∵k>0时,函数![]() 的图象是在第一,二象限的双曲线,且关于y轴对称,
的图象是在第一,二象限的双曲线,且关于y轴对称,
∴k>0时,当x<0,y随x增大而增大,x>0时,y随x增大而减小;
②∵k<0时,函数![]() 的图象是在第三,四象限的双曲线,且关于y轴对称,
的图象是在第三,四象限的双曲线,且关于y轴对称,
∴k<0时,当x<0,y随x增大而减小,x>0时,y随x增大而增大.
综上所述:k>0时,当x<0,y随x增大而增大,x>0时,y随x增大而减小;k<0时,当x<0,y随x增大而减小,x>0时,y随x增大而增大.

练习册系列答案
相关题目