题目内容
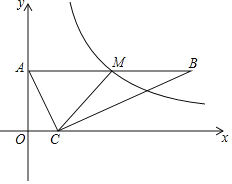
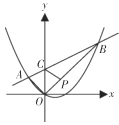
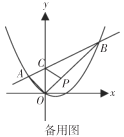
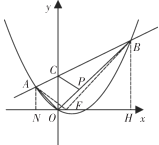
【题目】如图,在平面直角坐标系中,抛物线![]() 上有两点
上有两点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 到两坐标轴的距离相等.点
到两坐标轴的距离相等.点![]() 到两坐标轴的距离也相等.
到两坐标轴的距离也相等.
(1)求点![]() ,
,![]() 的坐标并直接写出
的坐标并直接写出![]() 的形状;
的形状;
(2)若点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,当
,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上一动点,当
轴上一动点,当![]() 是以
是以![]() 为斜边的直角三角形时,求点
为斜边的直角三角形时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;
;![]() ;直角三角形 (2)
;直角三角形 (2)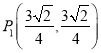 或
或![]() 或
或![]() (3)
(3)![]() ,
,![]()
【解析】
(1)设点![]() 的坐标是
的坐标是![]() ,代入
,代入![]() ,即可得到A的坐标,同理,可得到B的坐标,进而即可判断
,即可得到A的坐标,同理,可得到B的坐标,进而即可判断![]() 的形状;
的形状;
(2)先求出直线![]() 的解析式为:
的解析式为:![]() ,进而得到点C的坐标,再求出直线
,进而得到点C的坐标,再求出直线![]() 的解析式为:
的解析式为:![]() ,然后分3种情况:
,然后分3种情况:![]() 或
或![]() 或
或![]() ,分别求出点P的坐标,即可;
,分别求出点P的坐标,即可;
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .易证
.易证![]() ,得
,得![]() ,进而即可得到答案.
,进而即可得到答案.
(1)∵点![]() 在第二象限,
在第二象限,
∴设点![]() 的坐标是
的坐标是![]() ,
,
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,解得:
,解得:![]() ,
,![]() (舍去),
(舍去),
∴点![]() 的坐标是
的坐标是![]() .
.
同理可得:点![]() 的坐标是
的坐标是![]() .
.
∴∠AOC=∠BOC=45°,即:∠AOB=90°,
∴![]() 是直角三角形;
是直角三角形;
(2)设直线![]() 的解析式为:
的解析式为:![]() .
.
∴![]() ,解得:
,解得:![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵直线![]() 过点
过点![]() ,
,![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() .
.
∵![]() 为等腰三角形,
为等腰三角形,
∴![]() 或
或![]() 或
或![]() .
.
设![]() ,
,
①当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() (舍去).
(舍去).
∴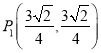 .
.
②当![]() 时,点
时,点![]() 在线段
在线段![]() 的中垂线上,
的中垂线上,
∴![]() .
.
③当![]() 时,由
时,由![]() ,解得:
,解得:![]() ,
,![]() (舍去).
(舍去).
∴![]() .
.
∴![]() 点坐标为:
点坐标为: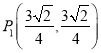 或
或![]() 或
或![]() ;
;
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
∵点![]() 为
为![]() 轴上一动点,
轴上一动点,
∴设![]() ,
,
当![]() 时,可得:
时,可得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.

练习册系列答案
相关题目